SUNY Geneseo Department of Mathematics
Friday, March 23
Math 223 04
Spring 2018
Prof. Doug Baldwin
(From this course plus some general comments from proofs)
Use of Canvas, organization of materials in it.
Open-notes exams.
Grading scheme, especially for exams.
Problem solving in class.
Face-to-face grading. I think this is important for giving immediate and timely feedback on your work, so I plan to continue doing it, even though some people listed it as something they’d like me to stop.
Solving problem sets as expected gets 80%, with more points for going “above and beyond.” This is frustrating to some people, but it sends an important message that meeting expectations isn’t perfection, and that you can rise beyond just meeting expectations, so I plan to keep doing it. But realize that given the way numeric grades convert to letter grades, you can also choose to do (only) what’s asked, get 80s on problem sets, and still probably get an A or B for the course, depending on how you do on the exams.
Face-to-face grading. See above
Solving problem sets as expected only gets 80%. See above.
Random names. I’ll use them as a backup mechanism for getting discussions going with wide participation, but will try first to run discussions through volunteers offering to speak. And random names results won’t be the only source of the “participation” part of your course grade.
Late penalties due to lack of time slots before “Grade By” date. Let me know by the “complete by” date if you can’t get an appointment, and I’ll work out some appropriate extension.
Review key points from readings at start of class. I don’t do this explicitly, but try to do it via my choice of in-class exercises and “key points” sections in the notes.
Provide reviews before exams, including good textbook problems to practice on and sample exams. These are good ideas, and I can use some class time for reviews, as long as they’re based on your questions. I put the second hour exam from last time I taught this course on Canvas, although in looking it over I realize that a lot of the questions deal with topics that won’t be on our exam, so I plan to replace it with something more useful, and with solutions, over the weekend.
More explanation of muPad. Good idea, I’ll do it.
Use the whiteboard instead of computer for in-class notes. I can do this if you feel a strong need, but the cost would probably be no more Canvas notes -- recreating a complete set of electronic notes from ephemeral whiteboard ones is much more time-consuming than cleaning up electronic notes started before or during class.
Let students use the whiteboard to explain things. Excellent idea.
Put information on Canvas to help you estimate letter grades. Good idea, I’ll think about ways to do it. One way might be to put the numeric-to-letter grade mapping from last time I taught this course on Canvas.
Hour exam 2 is next Thursday, March 29.
It will cover material not covered on the first exam, through partial derivatives (e.g., curvature, arc length, multivariable limits, partial derivatives, tangents, etc).
The rules and format will otherwise be similar to the first exam, particularly the open-book, open-computer rule.
Finish the example introduced last class: find the absolute minimum and maximum for z = x3/3 - x2 + y2 + 2y on the region -3 ≤ x ≤ 3, -2 ≤ y ≤ 2.
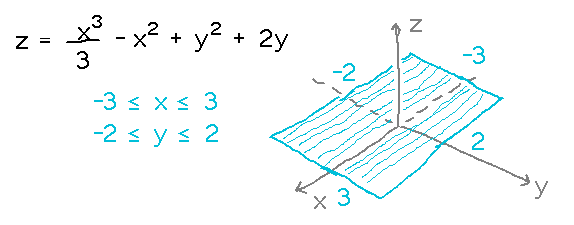
Procedure
Critical Points: Find the partial derivatives of z, and any values of x and y that make both 0 within the region -3 ≤ x ≤ 3 and -2 ≤ y ≤ 2:
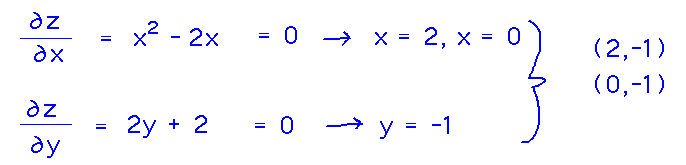
Boundary: Since this region has boundaries defined by constant values of x or y, you can set x or y equal to the appropriate constant in the equation for z, then find values of the other variable that minimize or maximize z just as you would for a single-variable function (i.e., take the derivative, look for places where it’s 0). While we’re doing that, also calculate the z values at the critical points we find and keep track of them for step 3:
We’ll finish this Monday by checking the corners of the region, getting z values for the critical points inside the region, and identifying the largest and smallest z values.
Optimization and Lagrange multipliers.
Read section 4.8.