The Chain Rule for Partial Derivatives

Return to Course Outline

Previous Lecture

Questions?

Problem Set

Partial derivatives and tangents, with a little bit from limits.

See the handout for details.

The Chain Rule for Multivariable Functions

Section 4.5.

Example

Find dz/dt given z = sin(2t) ln(t+1)

This looks like a pretty classic product-rule problem from single-variable calculus:

So what did it have to do with the chain rule? Another way of thinking about it is that z(t) is really composed of two simpler terms, say x and y, each of which is a function of t:

• x(t) = sin(2t)
• y(t) = ln(t+1)
• z(x,y) = x(t)y(t)

Now there’s a form of the chain rule that tells you how to find dz/dt:

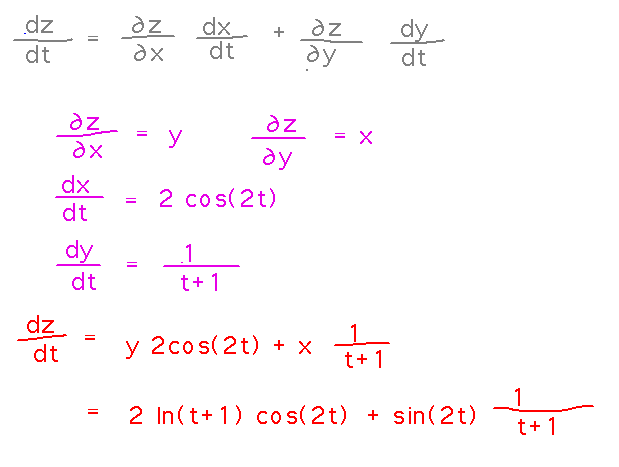
Example

Find ∂f/∂u and ∂f/∂v if f(x,y) = x²+y², x(u,v) = u sinv, y(u,v) = ve^u.

As above, you could substitute the definitions of x and y into the right hand side of f(x,y) and differentiate directly. Or you could use another form of the chain rule to work with simpler derivatives (albeit a larger number of them). For this latter approach, you first need the derivatives of f, x, and y:

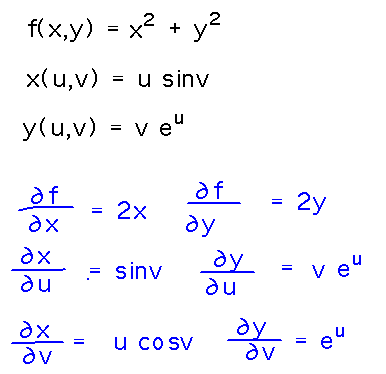
Then you can use the chain rule to combine these derivatives to get the final answers:

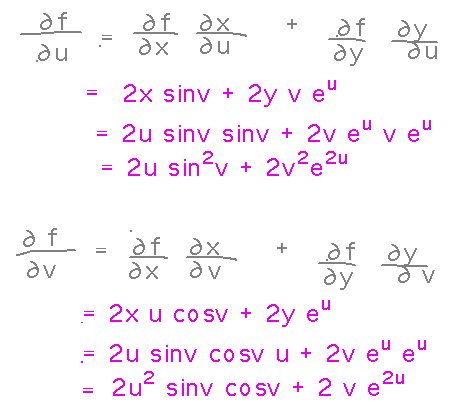
The Generalized Chain Rule

Yesterday we intuitively used the chain rule to find r_x(w,h) and r_y(w,h) for r(w,h) = √(w²+h²). Can you fit this into the terminology of the chain rule as generalized today and draw a tree diagram for it?

For example, yesterday you found a derivative something like this, using the chain rule intuitively on the expression inside the radical:

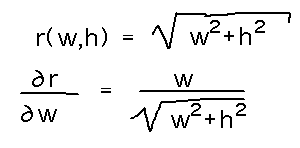
So explicitly think of the expression inside the radical as a function, i.e.,

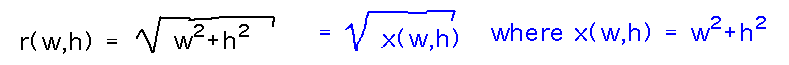
And now the chain rule as we have been talking about it tells you to think of the derivative of r with respect to w as the derivative with respect to x times the derivative of x with respect to w:

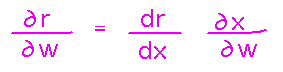
In tree diagram form, r is a function of a single intermediate variable, which in turn depends on two independent ones:

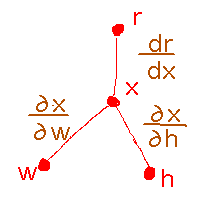
The general idea can be paraphrased as finding all derivatives of the dependent variable in terms of intermediate ones, multiplying by all derivatives of those intermediate variables in terms of others, and continuing in that manner until you reach derivatives in terms of the desired independent variable. Add together all the products thus obtained. Tree diagrams give a slightly more formal version of this idea. However you think about it, this idea unifies all forms of the chain rule, including the one for single-variable derivatives, and that unification is probably the most significant thing about the multivariable chain rule.

Key Ideas

The multivariable chain rule and how to use it in calculations.

But the real significance is in providing a unified way to understand differentiating any composition of functions in any combination of single- and multivariable forms.

Next

Directional derivatives.

Read the “Directional Derivatives” subsection of section 4.6.

Next Lecture