SUNY Geneseo Department of Mathematics

Directional Derivatives

Friday, March 9

Math 223 04
Spring 2018
Prof. Doug Baldwin

Questions?

Directional Derivatives

First subsection of section 4.6.

Intuitively, think of the directional derivative as being a projection of the derivatives with respect to x and y onto a direction not aligned with the x or y axes.

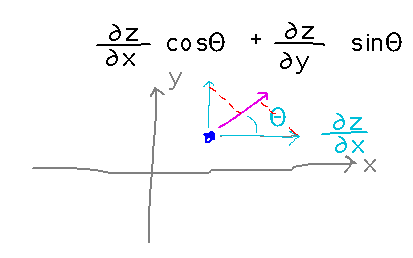
Direction vector with horizontal and vertical vectors projected onto it

Formally, the formula comes from the limit definition, which is based on the idea of change in z divided by corresponding change along the arbitrary direction vector, as the magnitude of the change along the direction vector goes to 0.

The vector version of the formula is based on the idea that the components of a unit vector (but only a unit vector) are the cosine and sine of its angle to the x axis.

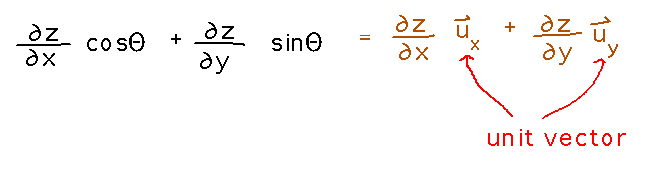
Derivatives times cosine and sine equal derivatives times x and y components of a unit vector

Practice

Find D_uz if z = 2x²y - 3xy³ and Θ = π/6 (so sinΘ = 1/2 and cosΘ = √3/2).

Start with the angle-based formula for a directional derivative:

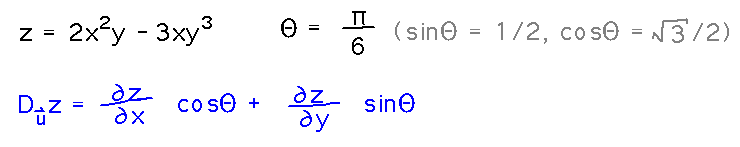
Directional derivative is dz/dx cos(Theta) + dz/dy sin(Theta)

Then find the derivatives of z, and plug them into the formula:

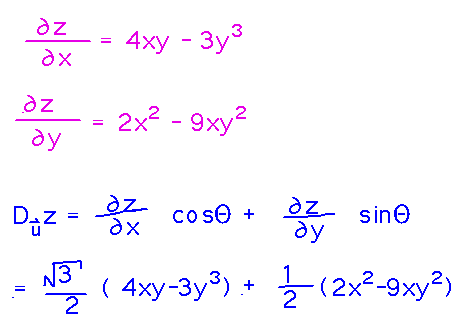
dz/dx = 4xy - 3y^3, dz/dy = 2x^2 - 9xy^2; directional derivative = sqrt(3)/2 dz/dx + 1/2 dz/dy

Variation

Find D_uz if z = √x - xy + √y and u = < √3/2, -1/2 >.

This time use the vector-based formula for a directional derivative (in other words, you can read the sine and cosine directly from the components of u).

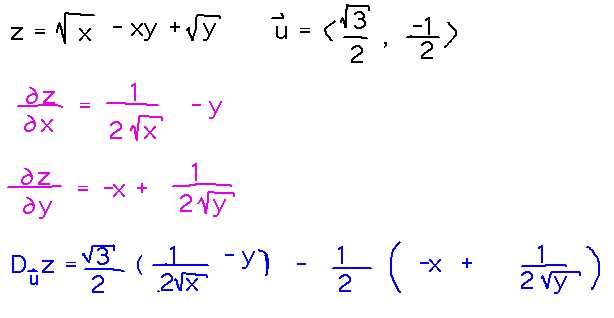
dz/dx = 1/2sqrt(x) - y, dz/dy = 1/2sqrt(y) - x; directional derivative = sqrt(3)/2 dz/dx - 1/2 dz/dy

Application

The number of gold widgets that Geneseo Widget Works can make in a day when they have g ounces of gold on hand and m widget-makers is 3m + g/2 - m²/100. If the Widget Works increases its gold supply from 500 ounces to 502 ounces, and its number of widget-makers from 100 to 102, by about how much will its widget output change?

The key idea is that this problem basically asks about the rate at which a function, call it w(m,g), changes with a change of inputs in a certain direction -- i.e., the directional derivative D_uw.

The change in inputs is from (100,500) to (102,502). Expressing this as a vector and then finding the unit vector in the same direction gives us the vector with which to find the directional derivative.

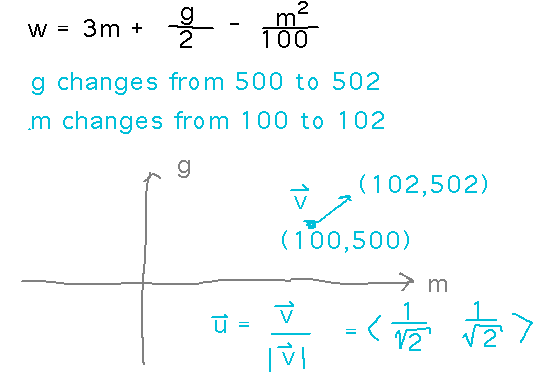
Vector from (100,500) to (102,502) in mg space

We’ll finish working out the actual number and thinking about what it means Monday after break.

Key Points

Directional derivatives as rates of change in a function with change in any direction in input. This generalizes partial derivatives, which are specifically rates of change in the x or y direction.

Formulas for directional derivatives with the direction as either an angle or a unit vector.

The gradient.

Read the “Gradient” through “Three-Dimensional Gradients and Directional Derivatives” subsections of section 4.6.

Next Lecture