SUNY Geneseo Department of Mathematics

Tangents and Linear Approximation

Wednesday, March 7

Math 223 04
Spring 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Problem Set 5

Beware of subtle (but correct) wording on question 3 - it’s not asking for the tangent to the curve.

GROW STEM Events

Title IX Workshop

Today, 4:00 - 5:00 PM, Newton 204

By Tamara Kenney, Geneseo Title IX coordinator

Club Interest Meeting

Tomorrow (Thursday, March 8), 5:00 PM, Newton 204

Part of creating a student organization focused on diversity in STEM fields.

Questions?

Tangents

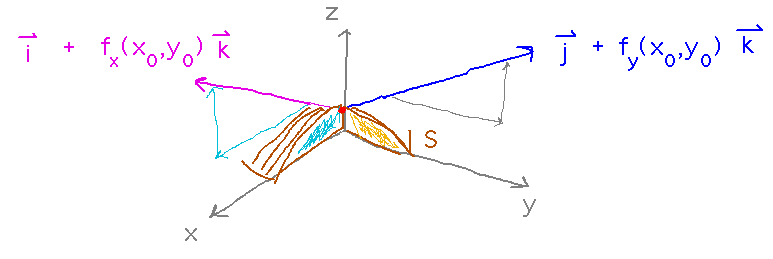
Where do the equations for tangent lines and vectors come from in the book’s derivation of the equation for a tangent plane (bottom of page 388)?

The “traces” are cross-sections through the surface, parallel to the x or y axis. Along each trace, x or y is constant, while the other variable can change. Thus the slope of the trace at any point is the change in z with y (or x) while the other stays constant, i.e., exactly what the partial derivatives are. The directions of these tangent lines are then vectors that change by fx(x0,y0) or fy(x0,y0) units in the z direction per unit change in the x or y directions, i.e., vectors with a unit i or j component, none of the other, and a k component dependent on the derivatives.

Cut-away view through surface with tangent lines parallel to x and y

Linear Approximation and Differentials

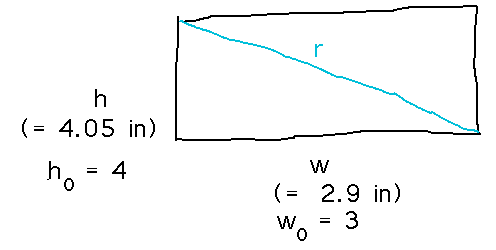
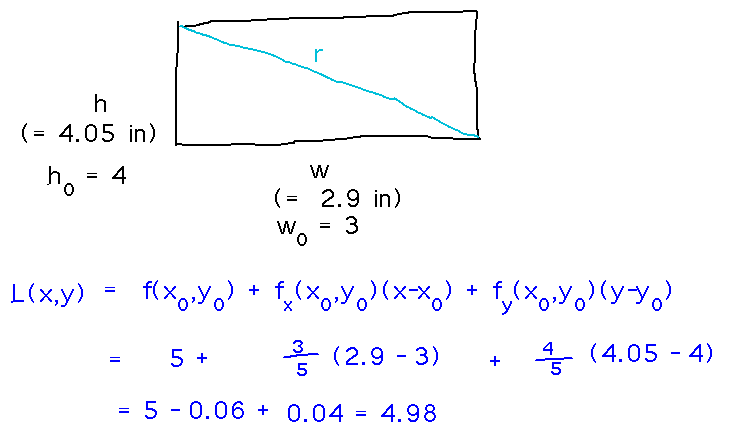
Consider a rectangle of height h and width w.

Use a linear approximation to estimate the length of the diagonal when h = 4.05 and w = 2.9 (hint: the length of the diagonal when h = 4 and w = 3 is easy to find).

Rectangle of height h and width w with diagonal

Find the equation for a linear estimate:

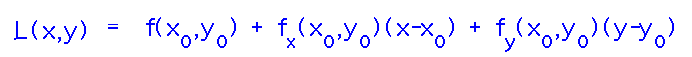
L(x,y) = f(x0,y0) + f_x(x0,y0)(x-x0) + f_y(x0,y0)(y-y0)

To use this, we need to know function f and its derivatives. Renaming a little, call the function r(w,h), since it finds the length r of the diagonal in terms of width and height:

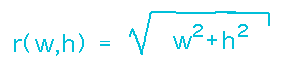
r(w,h) = sqrt(w^2+h^2)

Now we can find and simplify the derivatives:

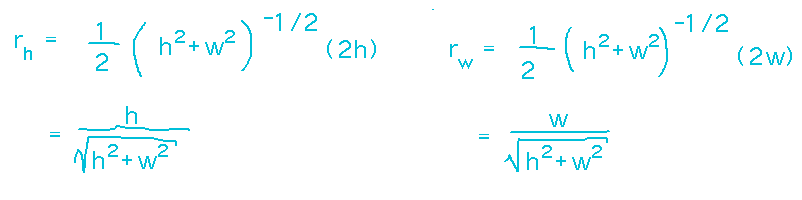
dr/dw = w/sqrt(w^2+h^2); dr/dh = h/sqrt(w^2+h^2)

And finally, plug in the known values for x0, y0, x, and y:

Rectangle with estimated diagonal

Key Points

Partial derivatives are slopes with only 1 variable changing.

Linear approximations via planes.

Next

The chain rule for partial derivatives.

Read section 4.5.

Next Lecture