SUNY Geneseo Department of Mathematics

Derivatives of Vector Valued Functions

Friday, February 9

Math 223 04
Spring 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Questions?

Derivatives of Vector Valued Functions

Part of section 3.2.

Differentiation Rules

What is the proof that the derivative of a vector valued function is the vector of derivatives of component functions?

If r(t) is a vector of r1(t), ..., rn(t) then r'(t) is a vector of r1'(t), ..., rn'(t)

Start with the definition of derivative for a vector valued function:

r'(t) is the limit as h approaches 0 of r(t+h) - r(t) all divided by h

Then expand the vector calculations in that definition:

The limit of vector function ( r(t+h) - r(t) ) / h is the limit of the vector of component functions

Now you can move the limit inside the vector...

The limit of a vector of component functions is the vector of limits of those functions

And finally notice that what you have inside the vector is just the derivatives of the component functions:

Vector of limits of (ri(t+h)-ri(t))/h is a vector of derivatives of the component functions

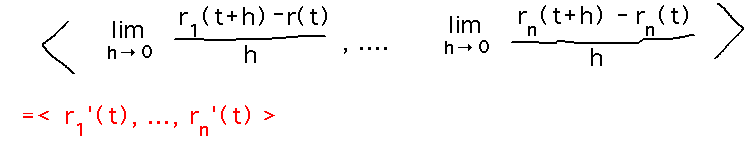
Find the 1st derivative of r(t) = 〈 2t2, esin t, √t 〉

How about the 2nd derivative?

Both of these use standard scalar function differentiation rules (e.g., the chain rule, the product rule, etc.) within the component functions:

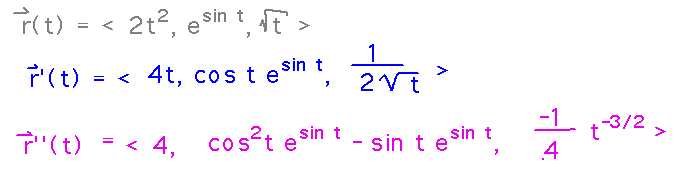
First and second derivatives of a vector function

What’s the 1st derivative of r(t)•s(t) if r(t) = 〈 1, t, t2 〉and s(t) = 〈 sin t, cos t, tan t 〉?

One way to do this is via the product rule for dot products, which is exactly analogous to the one for scalar products:

Derivative of r(t) dot s(t) is r'(t) dot s(t) + r(t) dot s'(t)

Another way would be to evaluate the dot product first, and then differentiate it as a scalar:

Calculate r(t) dot s(t) and then differentiate the result

Applications

What is the formula for the tangent vectors to our snake (s(t) = 〈 t, sin t, (t/6π)51 〉)?

The simple tangent vector function is just the derivative of the snake — much as with scalar functions, the derivative is tangent to the curve traced by a vector valued function.

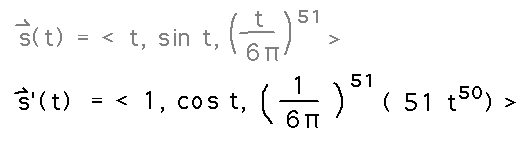
Derivative of the snake function

But this tangent is of who-knows-what length, and you often want a unit tangent vector (e.g., because we want to multiply it by some force to model parts of the snake’s motion). Compute the unit tangent vector by dividing the derivative by its magnitude:

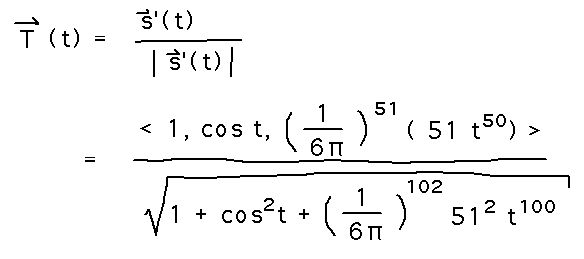
Snake derivative divided by square root of sum of squares of its components

Key Points

The limit definition of a vector valued function’s derivative and the equivalent form as a vector of derivatives.

Using scalar differentiation rules to calculate vector valued function derivatives.

Differentiation rules for vector operations such as dot or cross product.

Problem Set

See handout for details.

Next

Integrals of vector valued functions.

Read “Integrals of Vector-Valued Functions” in section 3.2.

Next Lecture