SUNY Geneseo Department of Mathematics

Integrals of Vector Valued Functions

Monday, February 12

Math 223 04
Spring 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

Conference

I will be out of town at a conference next Wednesday through Sunday (Feb. 21 - 25).

This is why the dates for the current problem set are so far in the future.

“Classes” for the 21st, 22nd, and 23rd will probably be a series of Canvas-based discussions designed to help you prepare for the first hour exam (which will be Monday Feb. 26).

Questions?

Derivatives of Vector Valued Functions

muPad can evaluate them via the diff function.

diff function produces a column vector of derivatives

Integrals of Vector Valued Functions

“Integrals of Vector-Valued Functions” in section 3.2.

Antiderivatives

Find the antiderivatives of r(t) = 〈 t - cos t, e2t, 1/t 〉.

The antiderivative of a vector valued function is just a vector of the antiderivatives of the component functions. So integrate each component, and then put them back into a vector:

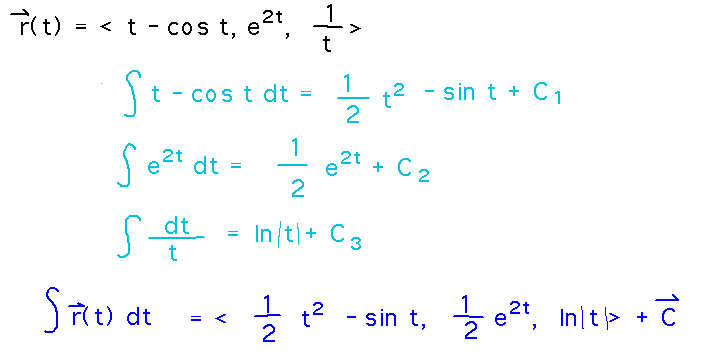
Antiderivatives of each component

Note that each component antiderivative has a distinct constant of integration. These can either be left in the components of the overall antiderivative, or pulled out into a vector constant of integration as done here.

Definite Integrals

Evaluate the integral from -1 to 1 of r(t) = 〈 t2, t + 1, e2t 〉.

Evaluate definite integrals by taking the antiderivative and then evaluating the resulting vector function between the bounds of integration -- that you can do this is what the book means by its allusion to the Fundamental Theorem of Calculus applying to vector valued functions.

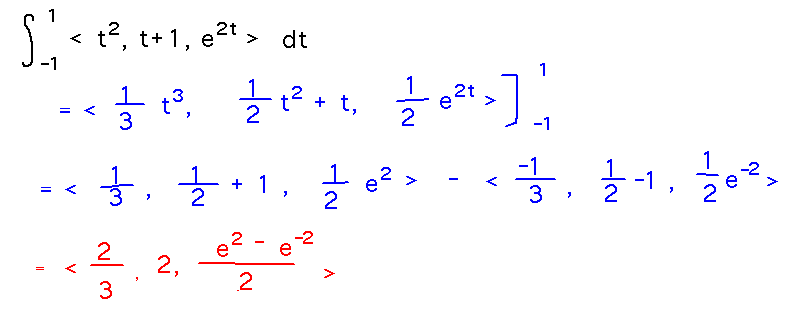
Antiderivatives at upper bound minus antiderivative at lower bound

Applications

Spacey the space traveler is flying with velocity v(t) = 〈 -sin t, cos t, 1 〉 m/sec. Assuming that Spacey’s position when t = 1 is r(1) =〈 1, 0, 1 〉meters from some reference point, find Spacey’s position and acceleration as functions of t.

Start by integrating veocity to get a position function:

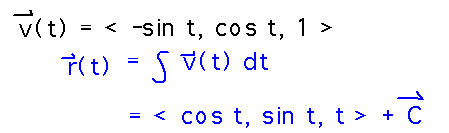
Antiderivative of vector function with unknown constant of integration

Now you can use the “initial condition” r(1) =〈 1, 0, 1 〉to figure out what the C vector must be:

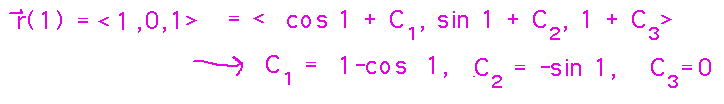
r(1) = <1,0,1> requires C1 = 1-cos(1), C2 = -sin(1), C3 = 0

Plug the components of C into the position function to get a final answer (or write the answer with a separate C vector with its components):

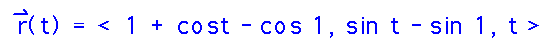
Antiderivative with C values filled in

Finally, find acceleration as the derivative of velocity:

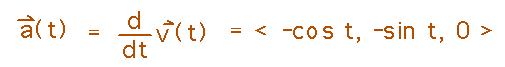
Acceleration is vector of derivatives of velocity

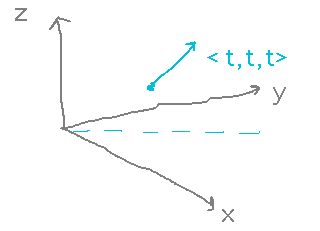
Consider the family of curves whose tangents are lines of the form 〈 t, t, t 〉. What do the equations for these curves look like?

3D coordinates with upward diagonal <t,t,t>

Since tangent vectors are derivatives of curves, take the antiderivative to find the basic curve equation:

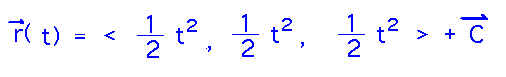
Antiderivative is <t^2/2,t^2/2,t^2/2> + C

Notice that since all 3 components of these vector functions are the same, the functions will all look like straight lines. What’s interesting about them is the meaning of the C constant of integration -- it determines where the lines are located in space, i.e., all solutions are parallel but at different places.

Key Points

The basic strategy is to integrate components.

Integration has applications to position/velocity/acceleration and similar problems.

Next

Arc length

Read the “Arc Length for Vector Functions” and “Arc-Length Parameterization” subsections of section 3.3.

(Note: the opening “recall Alternative Formulas for Curvature...” reference makes no sense here, but is probably a typo for “recall Arc Length of a Parametric Curve...,” which is a subsection in section 1.2 of our book that does provide some background for section 3.3.)

Next Lecture