Limits of Vector Valued Functions

Return to Course Outline

Previous Lecture

Questions?

Snake

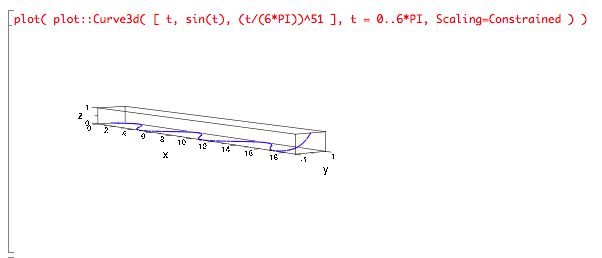
Another “snake” function, based on making the neck rise by raising a scaled t value to a high power, thus avoiding the very large numbers we saw yesterday. Scaling something to get a value that lies in a convenient range is a common trick.

s(t) =〈 t, sin t, (t/6π)⁵¹ 〉, 0 ≤ t ≤ 6π.

Limits & Continuity

Limits

Basic Idea

Find lim_t→1〈 t², (t²-1)/(t-1), tan(t-1) 〉

The limit of a vector valued function is just a vector of the limits of the component functions, so we can move the limit operation inside the vector and evaluate the components as separate scalar limits:

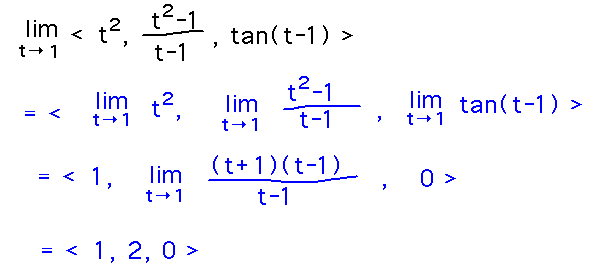
Does lim_t→0〈 ln t, 3t + 7, t / |t| 〉exist? No, because all component limits must exist for a vector valued function’s limit to exist. In this case the limits are undefined for ln t and t / |t|.

Limit Laws

Assume f(t) and g(t) are (3 dimensional) vector valued functions. Show that lim_t→c(f(t) + g(t)) = lim_t→cf(t) + lim_t→cg(t). Assume lim_t→cf(t) and lim_t→cg(t) exist, and let f(t) = 〈 f₁(t), f₂(t), f₃(t) 〉 and g(t) = 〈 g₁(t), g₂(t), g₃(t) 〉.

A good way to do lots of proofs, including this one, is to start with the definition of the thing you’re working with. In this case the key “thing” is a limit of a vector valued function, so let’s see if expanding that limit into a vector of scalar limits suggests anything:

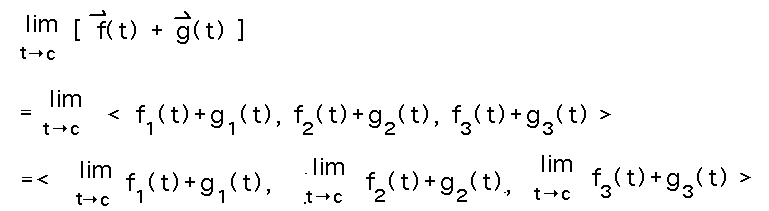
Now we can apply limit laws for scalar functions, and in particular the sum law:

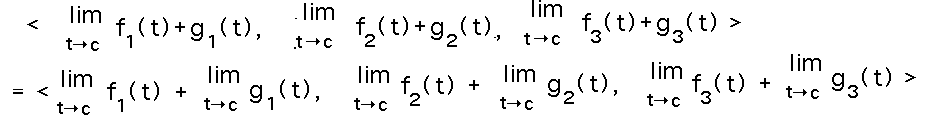
And now we have a vector that is the sum of two other vectors of limits:

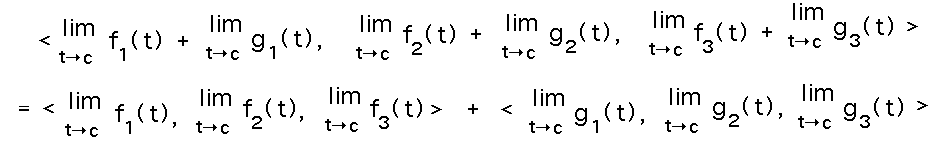
And finally we can use the definition of limit for vector valued functions “in reverse” to write each of the vectors of limits as a limit of a vector:

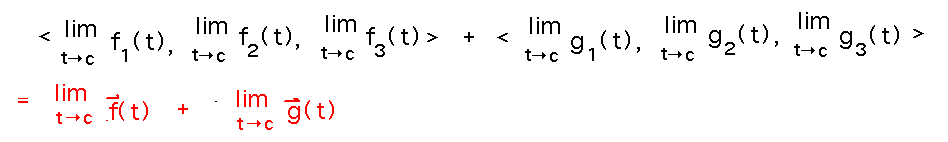
Continuity

Is 〈 (t²-1)/(t-1), t, 1/t 〉 continuous at t = 0?

For continuity, you need the same things you need for scalar functions:

• The limit at c exists.
• f(c) exists.
• f(c) = limit.

This function is not continuous because the 1/t component isn’t. Notice that because the definition for continuity for vector valued functions is essentially the same as for scalar functions, and because the value or limit of the vector valued function is just a vector of values or limits of scalar functions, you can summarize the rule for continuity as “a vector valued function is continuous at t = c if all of its component functions are.”

What about 〈 t+1, t, 1/(t+1) 〉at t = 0? Yes, this is continuous.

What about 〈 (t²-1)/(t-1), t, 1/(t+1) 〉at t = 1? This is not continuous because the (t²-1)/(t-1) is undefined at t = 1 (even though it simplifies to something that is defined at t=1; the original and simplified functions are different because the simplified one has one more point in its domain than the original).

Key Points

What the limit of a vector valued function is.

Using the definition to reason or prove things about vector valued limits.

The definition of continuity for vector valued functions.

Next

Derivatives of vector valued functions.

Read “Derivatives of Vector-Valued Functions” and “Tangent Vectors and Unit Tangent Vectors” in section 3.2.

Next Lecture