SUNY Geneseo Department of Mathematics

Spherical Coordinates

Monday, February 5

Math 223 04
Spring 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Questions?

Problem Set

Mostly about lines and planes, with a little on spherical coordinates.

See handout for details.

Spherical Coordinates

Warm-Up

Geneseo is at approximately 43 degrees north latitude and 78 degrees west longitude. What are the equivalent spherical coordinates, in a right-handed coordinate system with its origin at the center of the Earth, x axis aligned with the prime meridian, and z axis aligned with the North Pole? Earth’s radius is roughly 4000 miles.

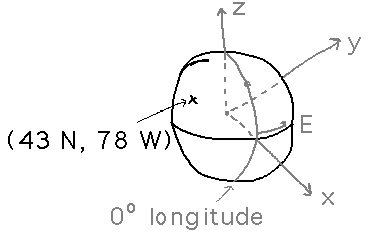
Earth with the equator and prime meridian and

This mainly requires converting a few conventions, e.g., the Φ angle is measured down from the pole, not up from the equator, and realizing that the Θ angle is measured from the x axis in the direction of y, which is east in this coordinate system. Then the spherical coordinates for Geneseo become (4000, 282, 47).

Earth with 43 N, 78 W = ( 4000, 282, 47 )

Spherical to Rectangular

What are Geneseo’s rectangular coordinates in the system described above?

Use the conversion equations given in the book to get x = 608, y = -2861, z = 2728 (rounded to whole numbers):

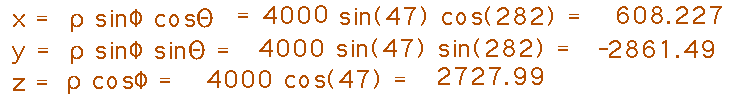
x = rho sin(phi) cos(theta) = 608; y = rho sin(phi) sin(theta) = -2861; z = rho cos(phi) = 2728

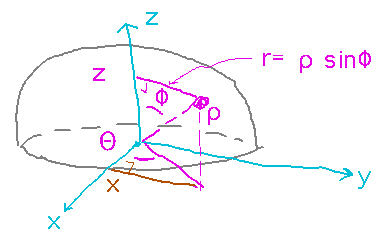
But where do these equations come from? Basically from using definitions of sine and cosine with triangles whose hypotenuses are radius distances and whose other sides are x, y, or z:

Hemisphere with radial line projected to z axis and to xy plane, that line projected to x and y axes

Rectangular to Spherical

Point (1,1,-√2) lies on the surface of the sphere x2 + y2 + z2 = 2. What are its spherical coordinates relative to that sphere?

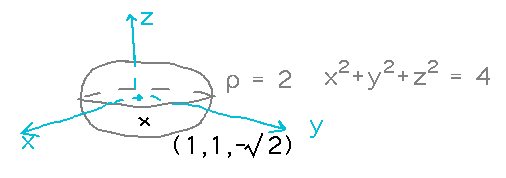
Sphere with radius = 2 and marked point (1,1, -sqrt(2))

Work out equations that are essentially inverses of the ones for converting spherical to rectangular (and are also in the book). It may be helpful to think of parts of these being based on equations for cylindrical coordinates (e.g., the use of the cylindrical radius r in finding ρ or the inverse tangent formula for Θ).

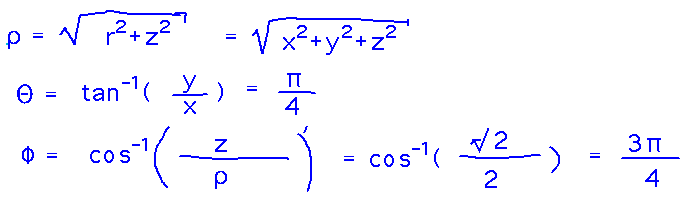
rho = sqrt(x^2+y^2+z^2); Theta = arctan(y/x); phi = arccos( z/rho )

Beware that the inverse tangent in this method needs to be interpreted carefully, since sometimes the angle you want is outside the usual range of inverse tangent. Use the rectangular x and y coordinates to guide you in deciding what xy quadrant the point is in.

Key Points

Spherical (and cylindrical) coordinates exist.

Converting between rectangular and spherical coordinates and vice versa. Both directions are ultimately based on using sine and cosine to project radial lines into the axes.

Next

Introduction to vector valued functions.

Read the “Definition of a Vector Valued Function” and “Graphing Vector Valued Functions” subsections in section 3.1.

Next Lecture