Planes

Return to Course Outline

Previous Lecture

Questions?

Planes

Part of section 2.5.

The Equation for a Plane

Three Points

Find an equation for the plane that contains (1,0,0), (0,1,0), and (0,0,1).

The basic idea is to take the cross product of any two vectors between points in the plane to get the normal, then use that normal and any one of the points to construct the plane equation.

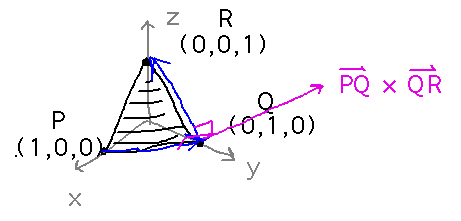
In this particular case, we can use the vectors between points P and Q and Q and R, giving 〈2,-2,1〉 as the normal:

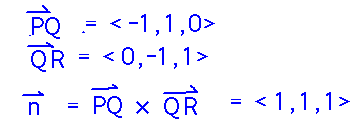
The components of this normal become the coefficients of the x, y, and z terms, respectively, in the standard plane equation; the coordinates of the point -- (1,0,0) here -- become the x, y, and z constants. The final plane equation is thus

Notice that there are two sides to a plane, and thus two normals. It doesn’t matter which you use to define the plane, so the equation could also be -x - y - z = -1.

Perpendicular Line and Point

Find an equation for the plane that contains (2,1,5) and is perpendicular to the line r(t) = (1,2,3) + t〈2,-2,1〉.

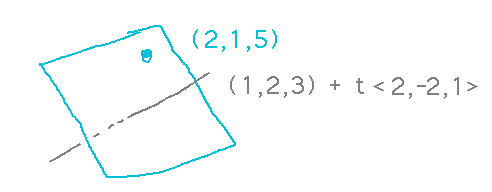
This is sort of a trick question, because unlike the book’s example the line is perpendicular to the plane, not in it. But that just means the line’s direction is normal to the plane.

Use that direction vector with the point in the plane to form an instance of the standard plane equation:

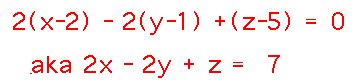
Reasoning about Planes

Describe how to find the equation for the line of intersection between 2 planes that doesn’t involve explicitly solving a system of equations for the direction vector (unlike the book’s example 2.52).

Since the line of intersection lies in both planes, it must be perpendicular to both normals. So its direction vector can be the cross product of the normals:

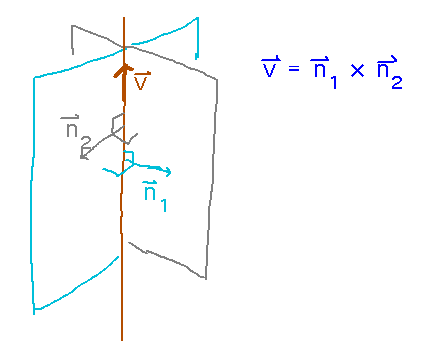
Apply this idea to book example 2.49 (the intersection of planes x + y − z = 3 and 3x − y + 3z = 5). Start by calculating the direction vector:

Now we need a point on the line. Any point that’s on both planes will do, so we have two equations to solve in 3 unknowns. Do this by picking any one of the variables and setting it to any convenient value. Usually 0 is good. This corresponds to finding the point at which the line passes through, say, the z = 0 plane (more generally, the plane corresponding to whichever variable you set to whichever convenient value).

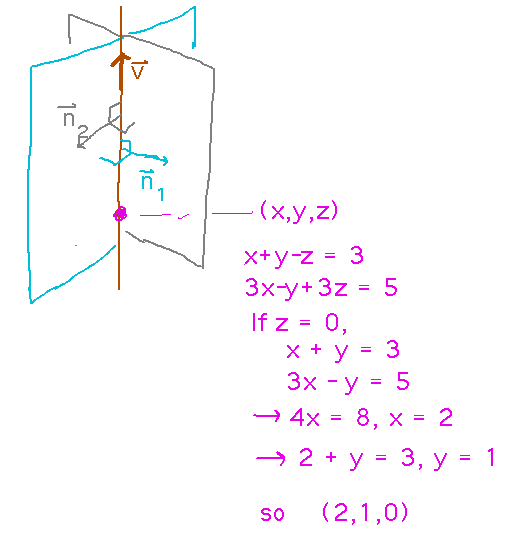
Finally, plug the direction vector and the point into the vector equation for a line to get

Key Points

The equation for a plane.

Connections between the plane equation and the plane’s normal vector lead to ways to solve lots of problems related to planes, their interactions with lines or other planes, etc.

Next

Spherical (and cylindrical) coordinates

Read section 2.7

Next Lecture