Misc
Geneseo Insomnia Film Festival
A festival of short films created by student teams over a 24 hour period. See https://www.geneseo.edu/insomnia or contact Joe Dolce (dolce@geneseo.edu) for details.
Extra credit for anyone in this class who works on a team that does a non-tutorial film with (accurate) math as a plot element.
Register for GIFF sooner rather than later, but in no case after March 16.
Questions?
Vector Valued Functions
Part of section 3.1.
Interpretation
What is the value of r(t) = 〈 t-1, t2, cos t 〉 when t = π? Plug in π for t to get〈 π-1, π2, -1 〉
Find some other points that lie on the curve r(t) = 〈 t-1, t2, cos t 〉. plug in any t, say 2, to get〈 1, 4, cos 2 〉.
Reasoning about Vector Valued Functions
Do the curves r(t) = 〈 cos t, sin t, t 〉 and q(t) = 〈 t, 1-t, 1-t 〉 intersect? If so, where?
In other words, are there are values s, and t such r(s) = q(t)? The vectors of equations for the two curves yield a system of 3 equations in 2 unknowns that you can solve to answer this (or try to, not all such systems will be solvable). If the s and t values you find are consistent, i.e., make all three equations hold, you have an intersection.

Plug the values for s and t into the respective vector function definitions to find the intersection point.
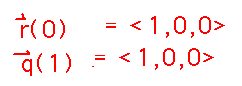
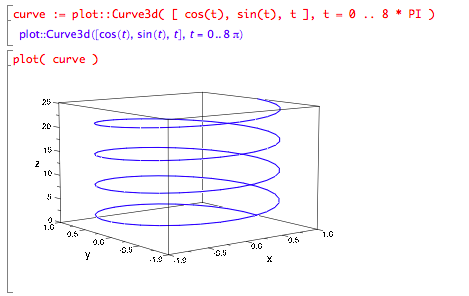
muPad
The basic plotting function for plotting 3D vector functions is plot::Curve3d.
Designing Vector Valued Functions
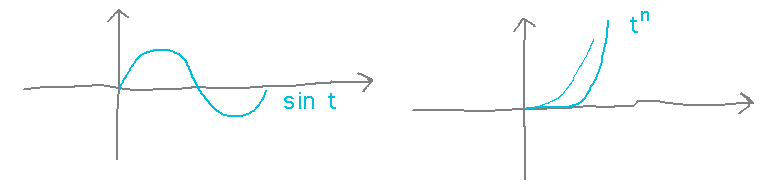
Can you come up with a function that provides a backbone shape for our computer animated snake?
Useful building blocks might be a sine curve, and the idea that high-degree polynomials are nearly 0 around t = 0 and then start rising rapidly around t = 1.
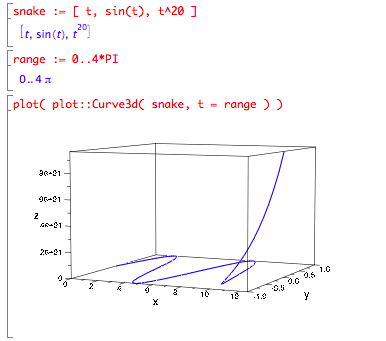
One realization of these ideas uses the function 〈 t, sin t, t20 〉 for 0 ≤ t ≤ 4π, and looks like this in muPad:
Key Ideas
What a vector valued function is, how it works.
The ability to reason about vector valued functions and their interactions, e.g., intersections.
The ability to design vector valued functions to follow certain curves.
How to plot vector valued functions with muPad or similar tools.
Next
Limits and continuity of vector valued functions.
Read the “Limits and Continuity of a Vector-Valued Function” subsection of section 3.1.