Cylinders and Quadrics

Return to Course Outline

Previous Lecture

Questions?

Cylinders

What’s going on with the definition of “cylinder” that allows any set of parallel lines through a curve to be a cylinder...?

It’s a generalization of the common definition of a cylinder as a round tube.

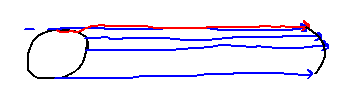
For example, think of a circle as a curve lying in a plane, and imagine drawing a bunch of lines through that curve (i.e., the edge of the circle), all parallel to the first line you drew. The result is what you informally think of as a cylinder:

Now think about generalizing this a bit, e.g., maybe the initial curve is more elliptical than circular:

You still get something pretty much like the informal cylinder, just not quite circular in cross-section.

Now take the generalization further, for instance to curves that aren’t closed:

Informally this might look more like a trough than a cylinder, but because it’s generated by the same definition as the other cylinders, it fits the mathematical definition of (general) cylinder.

Traces?

What’s a trace of a quadric surface?

Basically, a trace is a cross-section of the surface at a particular x, y, or z coordinate.

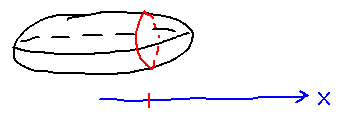
What are you supposed to do with the trace, e.g., in the book’s example (x² + y²/2² = z/5)?

This surface is an elliptical paraboloid, which we can see from the form of its equation, or from plotting it:

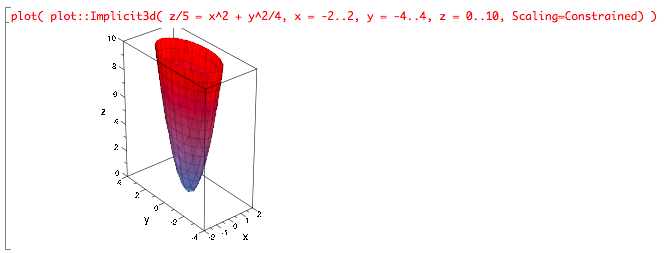
Various traces will give cross-sections of this shape. For example, setting x = 0 gives the x = 0 trace:

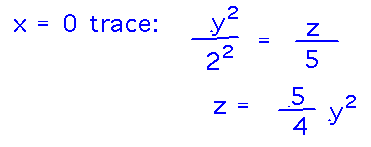
The trace doesn’t tell you specific values of the variables, but it is an equation you can recognize (at least probably more easily than you can recognize a 3-variable equation) as a parabola. That parabola is the cross-section of the surface in the x = 0 plane -- roughly what you see by looking at the curve with the x axis coming straight toward you.

Similarly, you can calculate the z = 5 trace:

This is the equation of an ellipse, giving you the cross-section of the surface as you look straight down the z axis (i.e., a cross-section perpendicular to the parabolic one you saw at x = 0).

Traces as cross-sections gives you some sense of how you might use traces: if you need to quickly estimate the shape of a 3D surface without having a graphing tool handy, the traces in each dimension can give you a quick general sense of what the surface looks like.

Cylinders

Which of the following define cylinders in 3 dimensional space? Graph each to see what it looks like.

x² + z² = 4

y = 2z

z = x² + y

All of these are general cylinders. One way to test that is to look at traces in dimensions perpendicular to the plane of the curve, and check to see if they are straight lines. For instance, the third example seems to be a parabola in the xz plane; are its traces produced by holding x (or z; to be really sure it’s a cylinder you should do both) constant parallel lines?

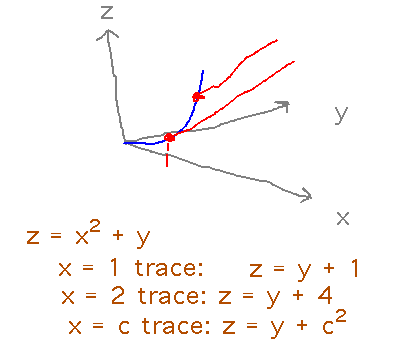
Since all these traces are straight lines (i.e., equations of the form z = mx + b) with slope 1, they are indeed parallel lines, suggesting that this is a cylinder.

You can also graph the surface to check visually if it looks like a general cylinder:

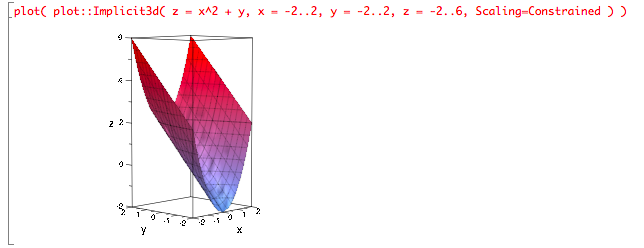
Problem Set

See handout for details.

Next

Introduction to vectors in 3 dimensions.

Read the “Working with Vectors in R³” part of section 2.2.

Next Lecture