SUNY Geneseo Department of Mathematics

Introduction to Vectors

Thursday, January 25

Math 223 04
Spring 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Questions?

Scalars vs Vectors?

Vectors have a magnitude and a direction, as in “I walked 5 feet diagonally left to get to my coffee.”

Scalars just have magnitude, as in “I paid 5 dollars for my coffee.”

Unit Vectors?

Any vector with length 1 is a unit vector, it doesn’t have to be parallel to the axes.

Vectors

“Working with Vectors in R³” from section 2.2

Standard Unit Vectors

What are the standard unit vectors and how would you express ⟨3,5,-2⟩ in terms of them?

i = ⟨1,0,0⟩

j = ⟨0,1,0⟩

k = ⟨0,0,1⟩

⟨3,5,-2⟩ = 3i + 5j - 2k

Momentum Example

A ball of mass 2g moving with velocity ⟨1,-1,2⟩ m/sec collides with a ball of mass 4g moving with velocity ⟨1,2,2⟩ m/sec.

After the collision the 2g ball has velocity ⟨1,1,1⟩ m/sec. Find the velocity of the 4g ball.

Background information: Momentum is the vector quantity mass times velocity. It is conserved in collisions, i.e., the total momentum of the 2 balls above must be the same after they collide as it was before.

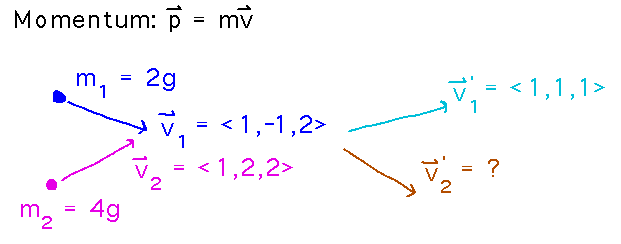
2g w/ velocity <1,-1,2> collides with 4g w/ velocity <1,2,2>

The first step is to figure out the total momentum of the system before the collision, which must also be the total momentum afterwards. These calculations involve computing scalar products and vector addition.

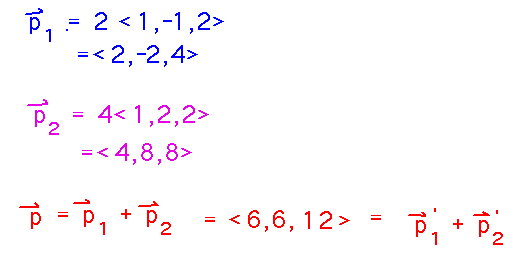
p_1 = 2<1,-1,2> = <2,-2,4>; p_2 = 4<1,2,2> = <4,8,8>; p = p_1+p_2

Now we can calculate the momentum of the first (2g) ball after the collision:

Since we know the total momentum after the collision, and the momentum of the 1st ball, we can calculate the momentum of the second ball by subtracting the first ball’s momentum from the total:

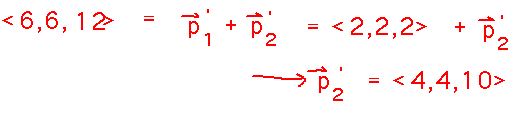
<6,6,12> = <2,2,2> + p'_2 so p'_2 = <4,4,10>

Finally, since the second ball’s momentum is 4 (its mass) times its velocity, we can divide its momentum by 4 to get its velocity:

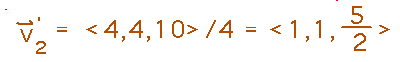
v'_2 = <4,4,10>/4 = <1,1,5/2>

As another question, what is the speed of the second ball after the collision? Speed is the magnitude of velocity (i.e., how fast but not what direction), so use the magnitude formula to calculate it:

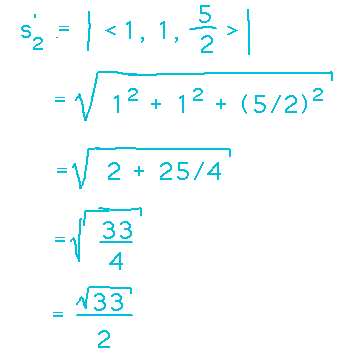
s'_2 = sqrt( 1^2 + 1^2 + (5/2)^2 ) = sqrt(33)/2

Video Game Example

First-person video games typically define their virtual worlds relative to some fixed coordinate system, but also need to know how the player is oriented in that system so they can do things like “move forward,” “look right,” etc.

For example, I’m standing at (1,1,1) relative to the coordinate system at the front of the room. Looking straight ahead I see the projector at (6,-6,4). Find a unit vector that describes the direction I see as “forwards.”

First, figure out the vector from me to the projector by subtracting my coordinates from the projector’s:

(6,-6,4) - (1,1,1) = <5,-7,3>

Now we can divide this vector by its magnitude to find a unit vector pointing towards the projector. So find the magnitude of the vector to the projector:

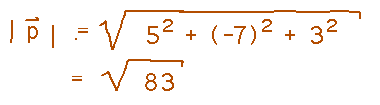
|<5,-7,3>| = sqrt( 5^2 + 7^2 + 3^2 ) = sqrt(83)

...and use it to calculate the unit vector:

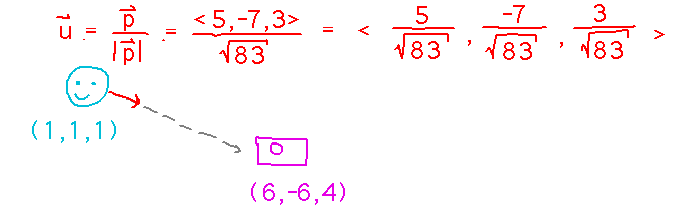
u = v/|v| = <5/sqrt(83), -7/sqrt(83), 3/sqrt(83) >

Take-Aways

Realize how standard unit vector and component notations are equivalent.

Vector arithmetic: addition, scalar product (including product with a fraction as division), subtraction.

Vector magnitude aka length.

How to find a unit vector in the same direction as a non-unit one.

The vector dot product.

Read section 2.3.

Next Lecture