SUNY Geneseo Department of Mathematics
Friday, January 19 - Wednesday, January 3
Math 223 04
Spring 2018
Prof. Doug Baldwin
Starts Monday (Jan. 22) at 11:30.
Hours are then generally Monday through Thursday mid-day and evening, plus Sunday evening.
See the MLC web site for details.
Right-handed vs left-handed coordinate systems? There are two ways the 3rd axis -- typically y -- in a 3D coordinate system can be oriented relative to the other 2:
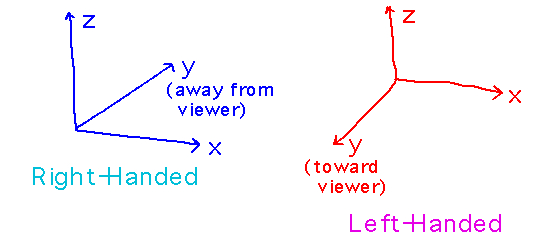
You can remember these orientations by how they line up with your hands: if you can point the fingers of your right hand along the positive x axis, curl the fingers towards the positive y, and have your thumb point along the positive z, it’s a right-handed coordinate system. If you have to use your left hand to do these things, the coordinate system is left-handed.
It generally makes no difference whether a coordinate system is right- or left-handed, but it’s convenient to agree on some handedness when talking about coordinate systems with others. Most people use right-handed as the default.
Parts of section 2.2.
Relative to the axes at the front of the room...
What are the coordinates of the tip of my nose? 5 units from the origin in the x direction and 1 in the y and z directions, so my nose is at point (5,1,1).
What are the coordinates of the tip of someone else’s nose? (4,-5,0) — note the negative y coordinate.
What’s the distance between them? Use the distance formula:
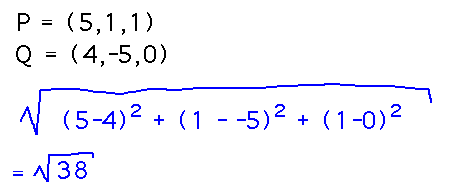
This calculation comes from the formula for the distance between points (x1,y1,z1) and (x2,y2,z2), namely
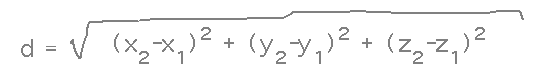
You can derive this formula (and similar ones for any number of dimensions) by using the 2D Pythagorean Theorem multiple times: first use it with, say, x and y distances to get a diagonal distance, then use that diagonal and the z distance to get a 3D distance, and so on if you have more dimensions.
How could you describe a region of space in which you are all sitting? There are lots of possibilities, including describing the range of x, y, and z coordinates occupied, finding equations whose graphs enclose the region, saying which octants you’re sitting in, etc.
In octants, you’re in the (+x,-y,-z) and (-x,-y,-z) octants.
What are the common ideas underlying the problems you just solved?
Scaling up ideas of locating points in 2 dimensions via distances along 2 axes to locating points in 3 dimensions via distances along 3 axes.
A neat way to think about this is that the lines that divide 2D space have become planes that divide 3D space, and the linear distances along those lines have become a grid on the planes (the grid defined by whichever 2 axes lie in each plane).
The notions of point coordinates, distance, and region that you used to solve today’s problems follow from the scaled-up ways of measuring position.
See handout for details.
“Complete by” is when I’ll feel free to give you another problem set, and will stop being sympathetic if you aren’t ready to grade this one.
“Grade by” is the latest you can meet with me to show me your work.
You don’t need to turn anything in before this meeting.
There are too many of you to all grade on that “Grade by” date. Schedule appointments soon to be sure you get a time you like, and be prepared to meet Thursday or Wednesday if you have to.
Google calendar demonstration.
Introduction to graphing 3-dimensional equations with muPad.
Please have Matlab/muPad installed on your computer before class, and bring that computer to class.