SUNY Geneseo Department of Mathematics
Thursday, January 18
Math 223 04
Spring 2018
Prof. Doug Baldwin
You are lightly graded, 0 to 5 points, as part of “Participation” when I call on you from the random names list, and the grade recorded in Canvas will be the average of the grades I give this way. Here’s a sense of how I come up with those grades.
What are the key things to remember about this syllabus and/or that you need more information about?
Problem sets: You’ll typically have around a week or a week and a half to do each problem set, with new problem sets coming out as soon as an old one is due. Grading will be via face-to-face meetings, and will focus on whether the combination of what you have written on your solution and what you say about it shows that you understand the concepts that the problem set is trying to exercise. If you change your mind about an answer in between writing it down and grading it, you can certainly say so in the grading meeting.
Hour exams: “Hour” is a misnomer, the exams will really take our normal 50 minute class time. This probably equates to between 4 and 6 questions. Like the problem sets, I generally expect you to be able to show that you understand what each question is testing; this means you can make arithmetic/typographical mistakes without losing many points -- whether those sorts of errors are present or not can make the difference between an 80% (what I expect) grade and 100% (perfect), but not between passing and failing a question. This is a less rigorous standard than I use for problem sets. Exam questions will be roughly comparable to middle-difficulty problem set questions.
Making appointments to see me for grading or anything else: The easiest way is through Google Calendar, which I’ll demonstrate as the first problem set comes due. But almost anything else that works for you is also doable, e.g., email me to set up an appointment, talk to me before or after class, etc.
Calculators: The required “calculator” is muPad, a piece of computer software (the helpdesk in Milne can help you install it if you have trouble). In general I think technology is moving away from dedicated devices like calculators and towards software that’s accessed via a phone app, web browser, etc., so the general “calculator” skills you should develop come down to being able to use muPad or Mathematica or some similar computer algebra system. You can use computers for such purposes on exams in this course.
Suppose you get a numeric grade of 70% on an exam. Roughly what letter grade does that correspond to? It’s in the middle of the B range. My grading system gives numerically lower grades than you may be used to, but I take that into account when mapping numeric grades to letter grades.
Where can you find material from this course online? Just about everything that I write down for this course goes into Canvas. In particular...
How much does the textbook cost? It’s free and available online.
Alice and Bob work together on a problem set. What should they do about it? Just acknowledge the shared effort -- as a general rule it’s better to work together to learn something than to not learn it while struggling by yourself.
How do you describe locations in 3D space? As (x,y,z) coordinate triples, adding a third dimension to the usual (x,y) coordinates:
Beware that this picture is good for the idea of taking the usual X-Y coordinate system and adding a third dimension, but mathematicians more commonly draw it with Z as the up-down axis and Y as the in-out one:
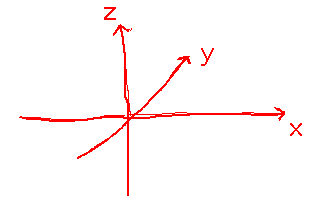
What if the space had 4 dimensions? Then you’d use 4-part coordinates, e.g., (x,y,z,w). (And it would be much harder to draw.)
Three dimensional space.
Read “Three Dimensional Coordinate Systems” and “Writing Equations in R3” in section 2.2