SUNY Geneseo Department of Mathematics
Monday, November 26
Math 223 01
Fall 2018
Prof. Doug Baldwin
“Errors, Eavesdroppers, and Enormous Matrices”
Dr. Jessalyn Bolkema, SUNY Oswego
Thursday, November 29, 2:30 PM, Newton 203.
Extra credit as usual for short reactions to the talk.
Last subsection of section 6.2.
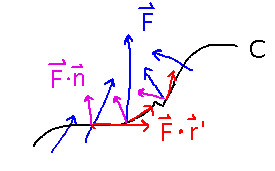
Two ways of looking at integrals of vector fields along curves.
What are those 2 views? The component of the field parallel to the curve ( F(r(t))·r′(t), circulation) and the component perpendicular to the curve (F(r(t))·n(t), flux).
Water circulates through a bag of grains as part of beer brewing:
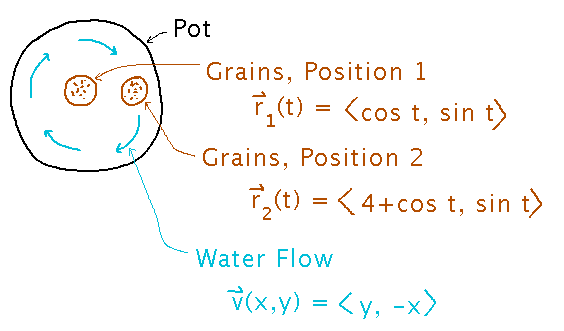
More water flowing through the grains is better.
What’s the flux through the bag at position 2?
Since this is a flux problem, start with the concrete computational form of a generic flux integral:
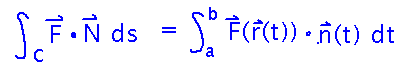
The n(t) vector comes from the derivative of the curve. Specifically, it rearranges the components of that derivative to ensure perpendicularity to it (check with a dot product), and to point to the right as seen from someone moving in the increasing t direction along the curve.
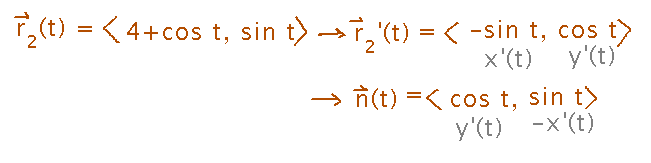
The bounds for the integral should be 0 to 2π, since we’re integrating one full turn around the circular bag. And now we’re ready to integrate:
The flux comes out to be 0 because the integral finds as much water flowing into the bag as flows out, and the two cancel. Not exactly what we wanted. To find the flow in, calculate flux across that part of the curve that water actually flows in through -- in this case, the top of the bag, i.e., the portion of r(t) between t = 0 and t = π.
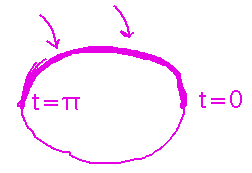
Most of the work of evaluating this integral has already been done, since F(r(t)) and n(t) are still the same. All that’s really changed are the bounds of the integral.
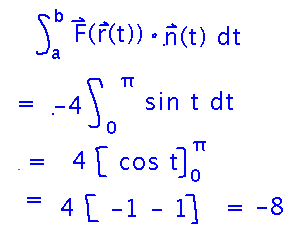
Now the flux is conveniently non-0. The negative sign means the flow is into the bag (since the way the curve for the bag is oriented, n(t) points out).
Some people calculated the flux into the bag at position 1, i.e., at the center of the pot. The flux here turns out to be 0, even over only part of the bag, because the water is circling around the center, i.e., flowing parallel to the sides of the bag at that position.
The idea of an integral of components of a vector field perpendicular to some curve.
The computational formula for finding such integrals.
How to find the necessary normal vector, n(t).
On vector line integrals in general, and their applications.
See handout for details.
Circulation.