Misc
Problem Set Grading
Did you think the outcomes-and-checkmarks grading system worked or didn’t for problem set 11?
SOFIs
aka Student Opinion of Faculty Instruction survey.
You should have gotten an email about filling them out through Knightweb.
Please do — your feedback can make a difference in how I teach this or other courses in the future.
Review Session
Do you want one for around an hour on study day?
The only rule would be that you come with questions or things you want to review, I won’t decide for you.
Questions?
Bounds?
What are the bounds of integration for problem set 12, question 1?
Start by parameterizing the path. Curves defined via an explicit equation with a single independent variable can be parameterized by making the independent variable be the parameter and the dependent variable the appropriate function of that parameter.

Once you have a parameterization, you can solve for the t values that make it equal to the starting and ending points:
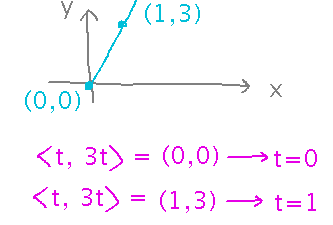
Differentials?
Now how do you use those bounds in the integral in question 1? Is it really 2 integrals, since there’s a “dx” part and a “dy” part?
You could separate it into 2, but realize that “dx” and “dy” can both be related back to t, thanks to the parametric form of the path.
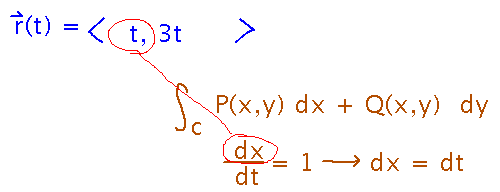
Circulation
Last class we looked at flux as a way of finding the flow of water through a bag of grains in brewing.
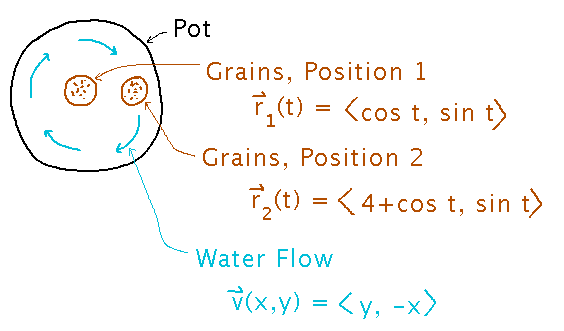
Circulation is less relevant to brewing, but what is the circulation around the bag at position 1?
Plug the curve for the bag and field for water flow into the standard form of a circulation integral and solve...
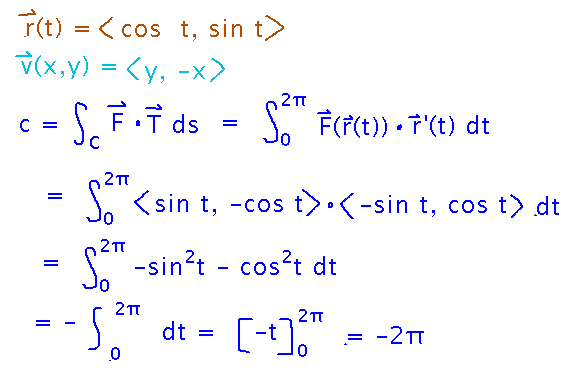
How is this integral different from the one for flux? The r′(t) vs n(t) difference is a big one, because it means flux integrals (with n) look at the component of a field perpendicular to the path, while circulation integrals (with r′) look a the component parallel to the path.
What if the bag is a slightly different shape?
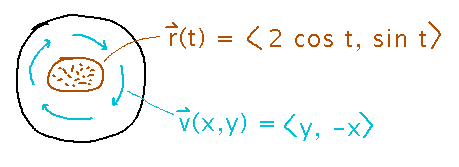
Not really different from before, just a different equation for the bag:

Key Points
Circulation formulas
Next
What if the flow of water changes in the above circulation examples?

Visually, based on idea of circulation as field parallel to path or tendency of field to make the region inside the path rotate, it seems it should be 0.
Can you find a position or shape for the grains that gives a non-zero circulation? Think about this quantitatively, i.e., via circulation integrals.
Then read about conservative vector fields, specifically...
- “Gradient Fields” in section 6.1
- “Curves and Regions” in section 6.3
- “Fundamental Theorem for Line Integrals” in section 6.3