Vector Line Integrals

Return to Course Outline

Previous Lecture

Misc

Hour exam 2 is graded. See me to get yours if you didn’t get it in class today.

This was a hard test, and the thing that made it hardest was the questions about level curves and derivatives.

Questions?

Solution to hour exam question 4?

This was the question that told you y = f(x) and x = g(u,v) and asked you to find ∂y/∂u.

This is a derivative of an outer function in terms of an inner variable, so the chain rule seems useful. Construct the right expression from this tree diagram:

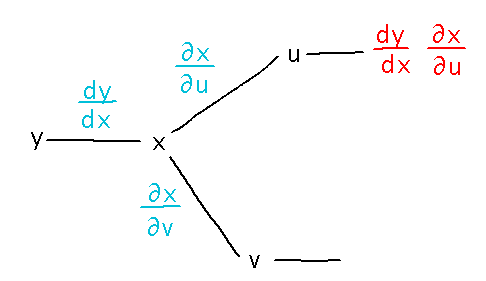
The only branch that ends in a “...∂u” is the upper one, from which you can read off ∂y/∂u = dy/dx ∂x/∂u.

Line Integrals in Vector Fields

Rolling ball sculptures: work done on a ball following a path. Suppose the ball weighs 1 ounce and distances are measured in inches (so work is in “inch-ounces”).

Connections to Reading

Work done by a force can be calculated as a Riemann sum of the dot product of force at specific points with small vectors in the direction of motion at those points. “Small vectors in the direction of motion” are the unit tangent vectors to the curve, scaled by ds. Turning the Riemann sum into an integral and realizing that the dot product produces a scalar means that we have a scalar line integral, but some simplifications are possible that mean this particular form of line integral is conveniently thought of as its own thing, with it’s own formula for evaluating it.

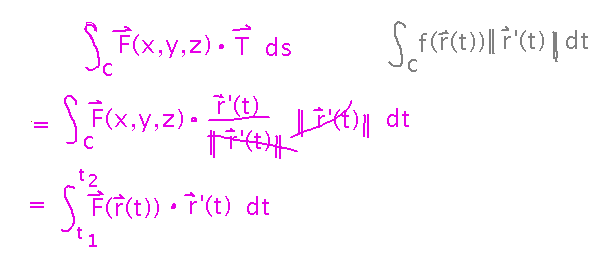
Gravity over a Helix

For example, how much work does gravity do on a ball rolling down the helix r(t) =〈 sin(πt), cos(πt), 4-t 〉, 0 ≤ t ≤ 4? The force on the ball in this case is constant 〈 0, 0, -1 〉?

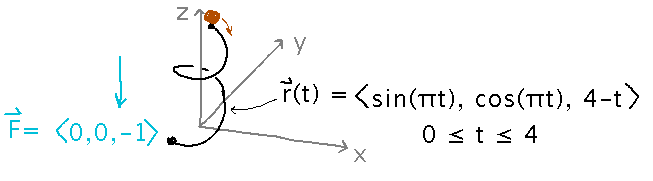
First of all, notice that expressing F in terms of r(t) doesn’t change F, because it doesn’t depend on x, y, or z: F(r(t)) = 〈 0, 0, -1 〉. With this realization, you can plug 〈 0, 0, -1 〉into the standard formula for a vector line integral to get

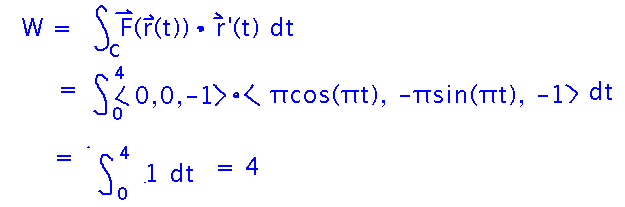
Gravity and Wind on a Parabola

What if there is a wind that gets stronger with height, w(x,y,z) = 〈 -z, 0, 0 〉, as well as gravity, and the ball is rolling down a parabolic segment z = x², y = 0 for -2 ≤ x ≤ 0?

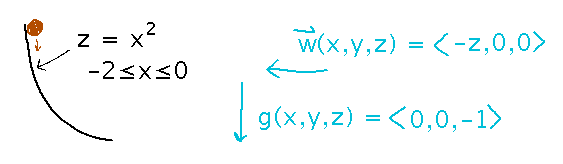
Here you need to start by finding a single force field by adding w and g (although you could solve this by doing separate integrals for each force and adding them at the end), and coming up with a parametric form for the parabola:

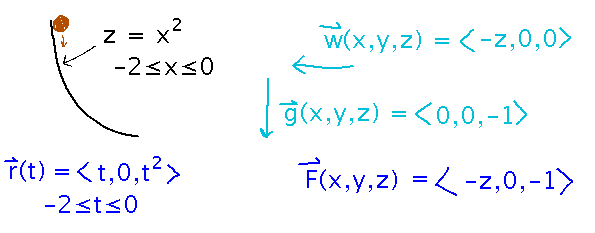
Now you can plug these into the formula for a vector line integral, with F(r(t)) being a little more interesting than in the first example, and integrate:

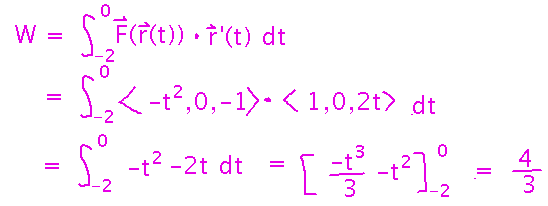
Key Points

What vector line integrals are.

Formula and process for evaluating them.

Next

Some other important applications of vector line integrals: flux and circulation.

Useful in brewing 2-dimensional beer:

Read “Flux and Circulation” in section 6.2 (and see if you can figure out what it has to do with brewing).

Next Lecture