Integrals over General Regions

Return to Course Outline

Previous Lecture

Misc

“Mid-Semester” Feedback

Simple questionnaire to return or not as you see fit.

Problem Set

On many recent topics, including extreme values, optimization w/ Lagrange multipliers, and multiple integrals.

See handout for details.

Questions?

Integration over General Regions

Section 5.2 and part of 5.4.

Cosine Example

Find the volume below the first half-cycle of z = cos(x+y) in the first octant

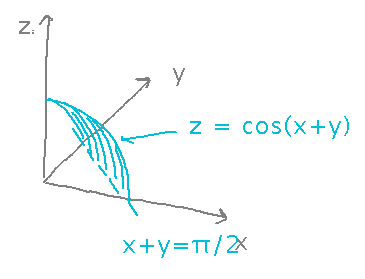
It’s helpful to think about exactly what part of the xy plane you want to integrate over:

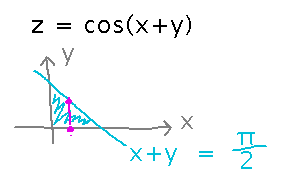
Then you can capture that region in the bounds of integration by making bounds on inner integral(s) depend on the variables introduced by outer ones. In this case, for any given x value, y can range between 0 and π/2 - x:

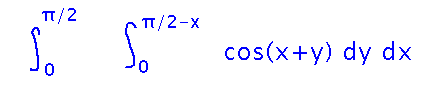
Finally, integrate just as you always have, just plugging expressions rather than constants in for some bounds:

Key Point

The idea of setting some bounds on iterated integrals be expressions that depend on the variables from outer integrals.

Next

Another Example

Integrate z = xy - 4x + y³ over the region bounded on the left and right by the curves x = -(y²+1) and x = y²+1, and above and below by the lines y = 1 and y = -1.

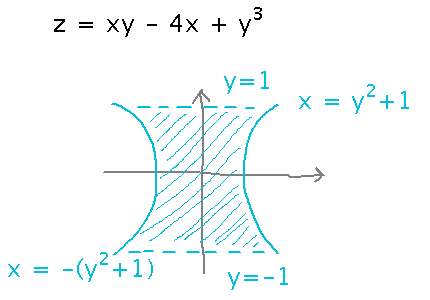
If there’s time, look at using multiple integration to find the area of the xy region.

Next Lecture