Questions?
Multiple Integrals
Section 5.1 (and a little bit from 5.4).
Question
Is there such a thing as a “partial antiderivative”?
Sort of. In the single-variable case there is an elegant relationship between definite integrals as geometric areas and indefinite integrals as antiderivatives:
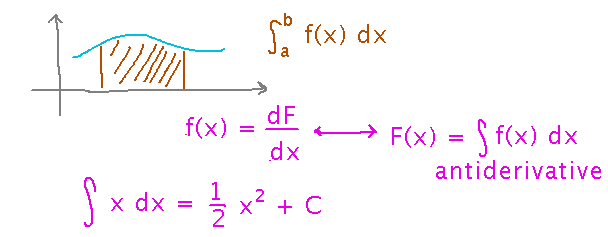
Antiderivatives (indefinite integrals) have a constant of integration in them, which makes the idea hard to scale to multivariable functions, since with multiple variables that constant becomes any function that doesn’t depend on the variable you’re integrating with respect to.
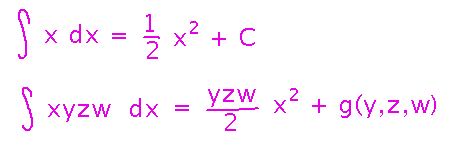
You may need lots of extra information to figure out what that function is. In a few weeks to a month we’ll see a situation where we’ll have the necessary information and will evaluate these antiderivatives, but people don’t do it nearly as often as they do for single-variable functions.
Example
What is the volume between the rectangle 1 ≤ x ≤ 2, -1 ≤ y ≤ 1 in the xy plane and the surface z = x2 + y2 + 2?
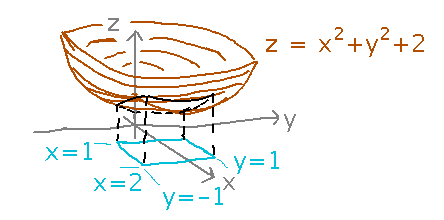
Calculate this as a double integral. The mysterious region R is just the rectangle over which x and y range.
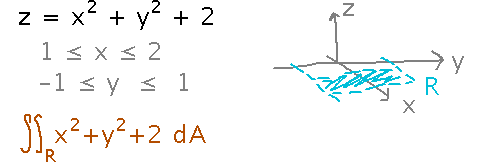
Express the double integral as an iterated integral, i.e., an integral of an integral, in order to evaluate it. In particular, as an iterated integral, you can evaluate it by evaluating the inner integral, treating all other variables as constants for the moment, then integrating the result for the outer integral.
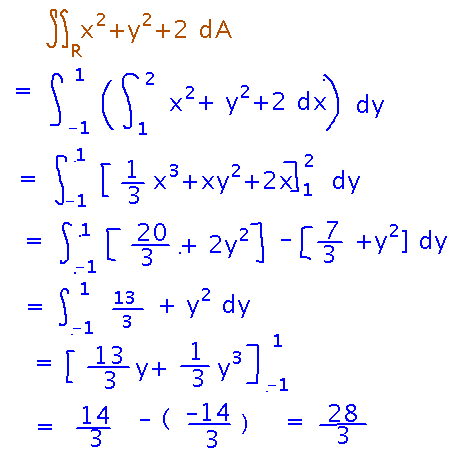
Multidimensional Example
What are the highest-dimensioned integrals in the real world?
In some of the computer graphics I do, integrals with 5 or more dimensions are common. In a technique called “ray tracing,” you integrate light coming from a patch of surface (3 position dimensions), taking into account how light sources reflect from that patch (2 direction angle dimensions).

Next
Multidimensional integrals over general regions.
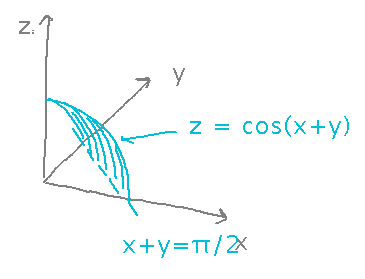
For example: Find the volume under the “first” half-cycle of the surface z = cos(x+y).
Read section 5.2 and “Triple Integrals over a General Bounded Region” in 5.4