SUNY Geneseo Department of Mathematics

More about Integration over General Regions

Monday, November 5

Math 223 01
Fall 2018
Prof. Doug Baldwin

Questions?

Problem Set Question 5

What is it asking?

One of the properties of double integrals is that if you have a 2-variable function that is really just a product of two 1-variable functions, then its integral over a rectangular region is the product of the integrals of the 1-variable functions over the corresponding ranges of values:

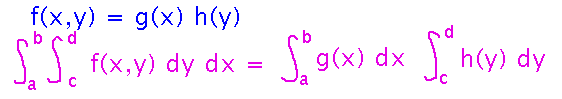
Integral of f(x,y) equals integral of g(x) h(y) equals product of integrals of g and h

If you expand the integral over region R into an iterated integral and think carefully about what terms are constant relative to which integration variables, you can rearrange the iterated integral into the right-hand side of this equation.

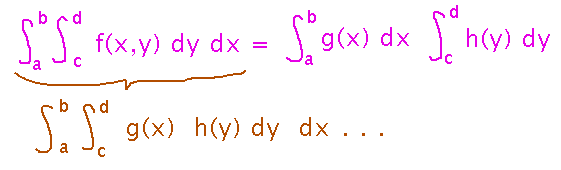
Integral of g(x) h(y) is integral over x values of integral over y values of g(x) h(y)

The question is asking you to show how to do this.

Problem Set Question 4

How do you set up the integral(s) over the region in question?

Clarified by the examples below.

Integration over General Regions

Section 5.2.

Example

Integrate z = xy - 4x + y³ over the region bounded on the left and right by the curves x = -(y²+1) and x = y²+1, and above and below by the lines y = 1 and y = -1.

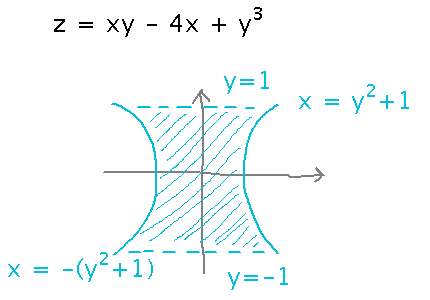
z = xy - 4x + y^3 and hourglass-shaped region in xy

Start by writing the abstract integral of z over the region as an iterated integral. Note that the outer integral is with respect to y, since the y bounds are constants, they don’t depend on any other variables. Then the inner integral is with respect to x, since the bounds on x have to be calculated from y. Any time you calculate bounds on some variable from the value of another, the other variable has to be defined outside the integral whose bounds are calculated.

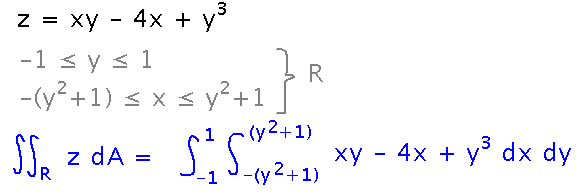
Integral from y=-1 to y=1 of integral from x=-(y^2+1) to x = y^2+1 of z

Once you have the integrals set up, evaluate them. Note that you substitute the expressions appearing in the bounds of the inner integral for x in the inner antiderivative, just as you would if those bounds were constants -- the algebra is messier, but at least in this case a lot of terms cancel out to keep the outer integrand fairly simple.

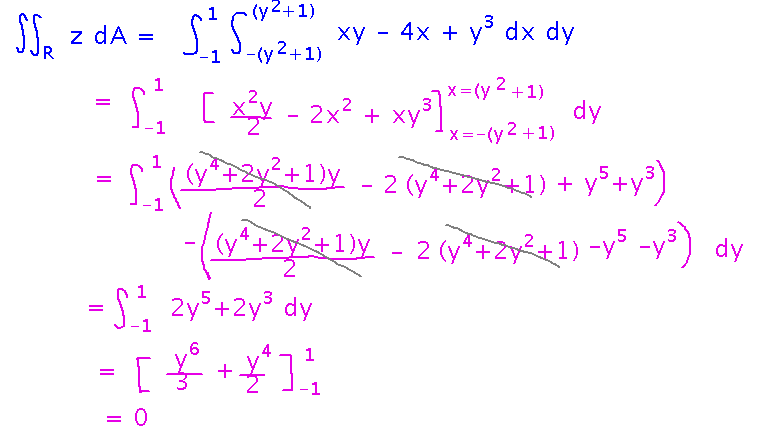
Substitute y^2+1 and -(y^2+1) for x in order to evaluate integral

Continuing the Example

Use multiple integration to find the area of the xy region.

Conceptually, the “dA” in integrals over areas represents an infinitesimally small bit of area (or more generally, n-dimensional space), so it makes some sense to think of the area (more generally, n-dimensional volume) of a region as the integral over it of that dA.

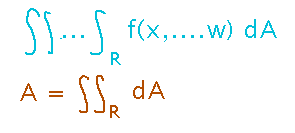
General integral over R is with respect to dA, i.e., differential area

To carry out this idea, set up the bounds of the iterated integral exactly as in the previous example (since it’s the same region), although the integrand is just “dx dy.”

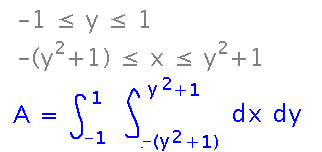
Area is integral from y=-1 to y=1 of integral from x=-(y^2+1) to x=(y^2+1) of dx dy

How does this compare to what you would have done with single-variable integration? To see, evaluate the inner integral:

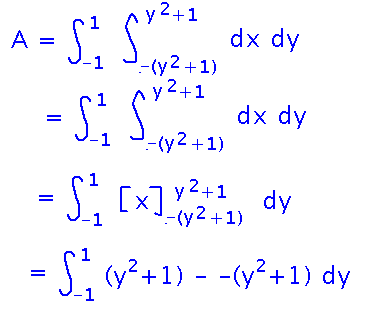
Area simplifies to integral of (y^2+1) - -(y^2+1)

The result is exactly what you would have used for an “area between two curves” problem in single-variable calculus. So you can interpret the single-variable technique as following from the multivariable view of area (there are other ways to think about where it comes from too).

Key Points

Setting up iterated integrals in the right order and with the right bounds — bounds reflect how the size of the region in some dimensions depends on your position within it in others, and order has to be one in which each variable used in a bound has been previously defined by an outer integral.

Evaluating iterated integrals, especially when their bounds are expressions rather than constants.

The connection between multivariable and single-variable area formulas.

Double integrals in polar coordinates.

Motivation: What’s the volume between the circle x² + y² = 4 and the surface z = 4 - x² + y²?

Read section 5.3.

Next Lecture