Geneseo Math 223 01 Optimization

Misc

Hour Exam 2

Monday (October 29).

Covers material since exam 1, e.g., arc length and curvature, multivariable functions, limits of multivariable functions, partial derivatives, tangent planes and linearization, the chain rule, gradients, directional derivatives, etc.

Rules and format otherwise similar to exam 1, especially open references and calculators rules.

A collection of practice questions, taken from past exams, is now available in Canvas.

Questions?

Proof Question

How to start the proof in question 1 on problem set 8.

Start by expanding f(x,y,z) in terms of r(t):

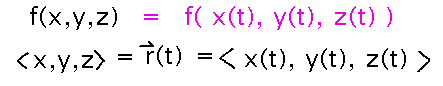
Since r(t) is vector x(t), y(t), z(t), f(x,y,z) is f( x(t), y(t), z(t) )

Then the chain rule seems like it will be helpful for dealing with df/dt. Keep in mind that all you need in the end is the gradient of f and the derivative of r, i.e., you do not necessarily need to find values for most of the derivatives that come up from the chain rule.

Use chain rule on f( x(t), y(t), z(t) )

3-Variable Limits

Any hints for how to work with limits involving 3 variables?

Showing that limits don’t exist by showing different limits along different paths gains even more flexibility, e.g., “paths” are often any path in a whole plane defined by setting 2 variables constant or assuming a linear relationship between variables, but the idea is similar.

Other tactics are also similar to those for 1- or 2-variable limits, e.g., algebraic simplification, plugging in values at the limit point.

Extra credit opportunity: I invented this limit off-the-cuff for discussion, which it turned out not to be very good for. Find its value, or show that the limit doesn’t exist. Based on discussion in class, my current guess is that the limit is 0, and that you will have to use the delta-disk definition of limit to show it.

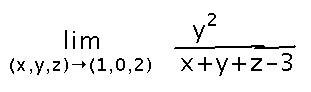
Limit as (x,y,z) goes to (1,0,2) of y^2 / (x+y+z-3)

Lagrange Multipliers

Section 4.8

Example

Geneseo Widget Works produces am/10 - m widgets per hour with a assemblers and m managers. If assemblers earn $15/ hour and managers earn $25/hour, and GWW can afford to pay $1000/hour in salaries, what’s the optimal number of assemblers and managers?

What does the reading give you for approaching something like this? The method of Lagrange multipliers, i.e., set the gradient of the objective function equal to some multiple (lambda) of the gradient of the constraint function, and solve for the relevant variables.

Start it.

Objective function am/10 - m; constraint 15a + 25m - 1000 = 0; gradient of f = lambda times gradient of g

Finish this for Wednesday

After exam.

Finish Lagrange multipliers.

Lagrange Multipliers and Optimization