More on Lagrange Multiplers

Return to Course Outline

Previous Lecture

Questions?

Lagrange Multipliers

Section 4.8

Example

Geneseo Widget Works produces am/10 - m widgets per hour with a assemblers and m managers. If assemblers earn $15/ hour and managers earn $25/hour, and GWW can afford to pay $1000/hour in salaries, what’s the optimal number of assemblers and managers?

Friday we identified the method of Lagrange multipliers as one way to solve this.

Finish it

Start by expanding the equation between the gradients:

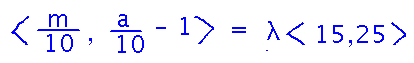
Then break it into a system of equations — corresponding components of the vectors must be equal in order for the vectors to be equal:

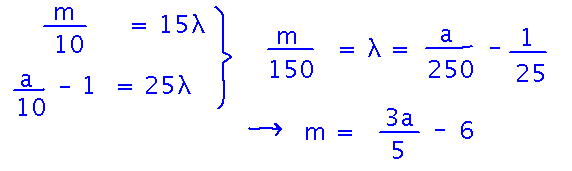
Here, we could find an equation for m in terms of a, which we can plug into the constraint to find a. Notice that we don’t actually need a value for λ.

Finally, use a to find m:

You can now plug a and m into the equation for w if you want to find the actual optimum number of widgets. It’s also a good idea to verify that this is a maximum rather than a minimum.

Another Example

Consider a vertical tube with its bottom end on the circle x² + y² = 4, z = 0, and its top end in the surface z = x² + y + 3. What are the maximum and minimum values around the top end?

Here the equation for z is the objective function, and the equation for the circle is the constraint on its inputs.

Set up the equation between gradients, and the corresponding system:

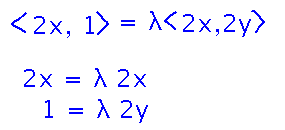
Now just divide the first equation by 2x to get λ=1, and then using that in the second equation to get y = 1/2, right?

Almost. Except when you divided by 2x, you were implicitly assuming x ≠ 0. You need to also see if there is a solution with x = 0, in which case you couldn’t divide by 2x to begin with, and have to find some other way of solving.

(In this case you can use the constraint to find that if x = 0 then that along with y = ±2 is also a solution.)

Key Points

The method itself.

Lagrange multipliers typically lead to an underconstrained system of equations to solve.

Lambda’s value may not be needed

The constraint provides extra information to resolve the underconstrained system.

Beware division by 0.

Next

Question: What is the volume between the rectangle 1 ≤ x ≤ 2, -1 ≤ y ≤ 1 in the xy plane and the surface z = x² + y² + 2?

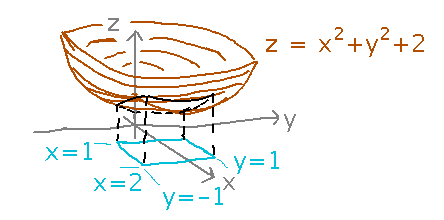
Read section 5.1 and “Integrable Functions of Three Variables” from 5.4.

Next Lecture