SUNY Geneseo Department of Mathematics

Directional Derivatives and Gradients

Friday, October 19

Math 223 01
Fall 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

PRISM Peer Advisement

Next Thursday, Oct. 25, 5:30 - 6:30, South 328.

Advice/talk from/with other students about the math major, course selection, gen ed, etc.

Questions?

Problem set 7 question 4? It doesn’t require you to explicitly find a tangent plane, although the equation for linear estimation is essentially the equation for a tangent plane.

Problem set 7 question 5? Estimate partial derivatives from the table.

Definitions

Section 4.6.

Field trip to Sturges Auditorium.

What is a directional derivative? The rate of change of a function as you move in a given direction through the space of its variables (e.g., through the xy plane for a function with variables x and y).

What is a gradient? There are several geometric interpretations of the gradient:

Gradient

Auditorium Example

Suppose Sturges Auditorium is a semi-circular tunnel, so the equation for the ceiling is z = √(400-4y2)

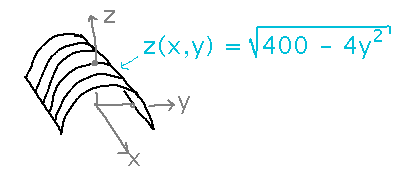
Tunnel with equation z(x,y) = sqrt(400-4y^2)

If you are standing at point (0,5), what direction should you walk in in order to have the height of the room over your head increase fastest?

Use the fact that the gradient points in the direction of greatest increase in the function’s value:

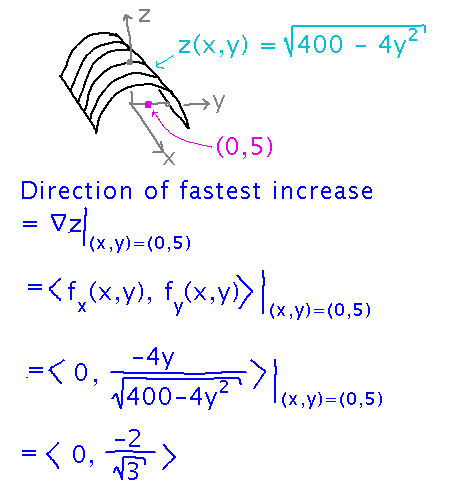
Gradient of z at (0,5) is the vector of partial derivatives with 0 plugged in for x and 5 for y, aka (0,-2/sqrt(3))

Note that this direction is towards the center of the auditorium, consistent with what you did when walking along gradients in the actual auditorium.

Cell Phone Example

Suppose you’re standing at point (0,0) in a cell phone signal “shadow” in which signal strength is given by s(x,y) = x ey. What direction should you walk in to get the fastest increase in signal strength?

Person with phone standing at origin of coordinate system

Once again, use the fact that the gradient gives you the direction of greatest increase:

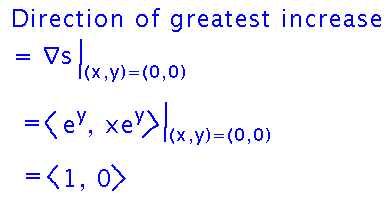
grad s is vector of e^y and x e^y, or vector (1,0) when (x,y)=(0,0)

By how much will the signal strength increase per unit of distance you walk in that direction? Use the fact that the rate of change (i.e., the value of the directional derivative) in the gradient direction is the magnitude of the gradient:

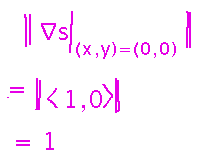
Magnitude of gradient is 1

Key Points

Calculate gradient as a vector of partial derivatives.

Definition/properties of the gradient.

Next

Some examples of directional derivatives.

Then local extreme values.

Guiding example: Where does the function f(x,y) = 10 - x2 - y2 + xy + 4x + 2 have its largest value?

Read these subsections of section 4.7:

Next Lecture