SUNY Geneseo Department of Mathematics

Partial Derivatives

Friday, October 12

Math 223 01
Fall 2018
Prof. Doug Baldwin

Questions?

When Multivariable Functions Don’t Have Limits

Show that lim_{(xy,z)→(0,0,0)} x/(y+z) doesn’t exist.

Analogous to how single-variable limits don’t exist if the limits from left and right differ, multivariable limits don’t exist if any paths that approach the point in question from different directions imply different limits. But now there are an infinite number of directions to approach from, not just 2.

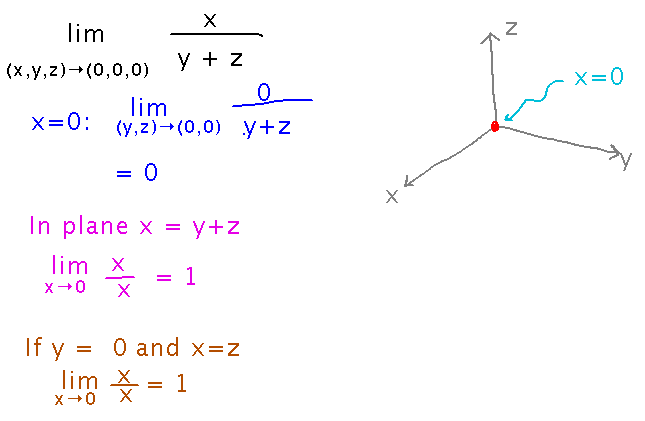
Different paths along which x, y, and z can approach (0,0,0) lead to different limit values

There is no L’Hospital’s Rule for multivariable functions!

Key Point

Use multiple paths to show that limits don’t exist

Derivatives of Multivariable Functions

Section 4.3.

Partial derivatives give you the rate of change of a function if one of its variables varies while the others stay fixed. What if several variables vary at the same time? Then you need a “directional derivative,” which we’ll talk about in a week or so.

Practice

Find the partial derivatives of f(x,y) = 3x²y³ - cos(x²+y³)

You can evaluate partial derivatives by pretending all variables except the one you’re differentiating with respect to are constants and then treating the problem as a single-variable derivative.

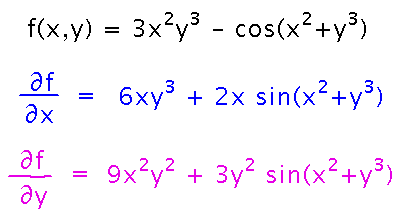
A function and its partial derivatives wrt x and y

How about g(x,y) = x^y

Use the same approach:

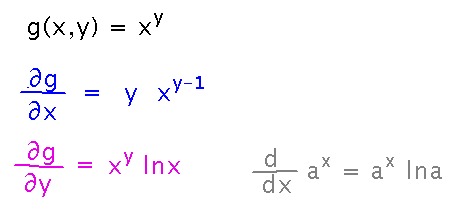
Derivative of x^y wrt x is y x^(y-1); wrt y it's x^y ln y

Mathematica

Mathematica’s D function takes partial derivatives (that’s why you have to specify the variable to differentiate with respect to).

For example, it agrees with us on the previous example (noting that log is the natural logarithm, despite not being called ln)

Problem Set

See handout for details.

Key Points

Evaluating partial derivatives by hand.

Evaluating them with Mathematica.

Second partial derivatives.

Then tangent planes and linearization.

Read section 4.4.

Next Lecture