Misc
Colloquium
“A User-Friendly Approach to Supervised Learning.”
Dr. William Cipolli, Colgate University.
Friday, October 19, 2:30 - 3:30, Newton 204.
Extra credit for writing roughly 1 paragraph about connections you make to the subject or talk.
Questions?
Problem 2
How to decide whether the limit in the problem does or doesn’t exist, and if it exists, how to find it?
Use intuition to decide whether to start with the hypothesis that it exists, or the hypothesis that it doesn’t. Then gather the techniques you have for showing whichever you pick, and try to deploy them. But be prepared to switch guesses if the initial one doesn’t seem to be working.
Initial guess is that this limit doesn’t exist. But several attempts to show that it has different values as you approach (0,0) along different paths repeatedly lead to an indeterminate 0/0. Despite being indeterminate, this is actually suggesting that the limit does exist because 0/0 could correspond to a definite limit, and the two path test isn’t producing actual numbers you can use to show that the limit doesn’t exist.
So switch to trying to find the actual limit. The denominator is awkward with the square root, but the square root could be removed by multiplying the denominator by its conjugate, so try that:
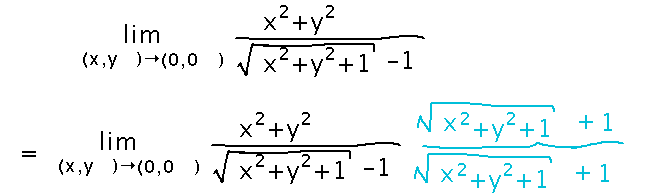
Now the function inside the limit simplifies via cancellation until it’s in a form you can plug the limit point into without getting 0/0:
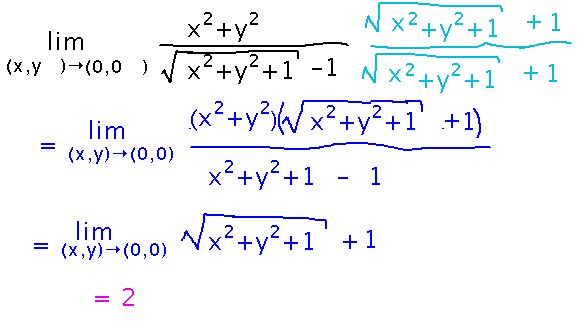
Problem 1
What is it asking?
Recall that level curves are curves in the xy plane along which f(x,y) has a constant value. The question asks you to write equations for, and draw a graph of, three level curves. The “c =” phrases are just telling you what the constant should be for each level curve.
Problem 4
Asks you to generalize the definition of an infinite limit of a single-variable function to one of an infinite limit for a two-variable function.
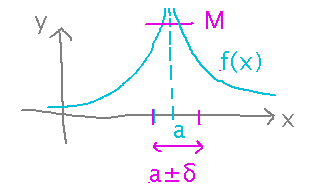
The key idea behind this generalization is to replace the δ-unit-wide interval in one dimension with a δ-disk in two dimensions.
Higher-Order Partial Derivatives
Find all the 2nd derivatives of f(x,y) = x siny - y sinx
There are 4 such derivatives, corresponding to taking 2 possible derivatives of each of 2 possible first derivatives:

Notice that the two mixed second derivatives are equal. This is a consequence of Clairaut’s Theorem.
Key Point
Second (and higher order) partial derivatives are partial derivatives of partial derivatives, exactly analogous to higher-order single variable derivatives.
Next
Tangent planes and linearization.
Read section 4.4.
Guiding problem: The formula for the length of a rectangle’s diagonal is a function of width and height. What is the tangent to the plot of this function with width = 4 and height = 3 cm? Use a linear approximation to estimate the length of the diagonal when width = 4.05 and height = 2.9 cm.
