Questions?
Problem set question 3?
The question asks where an ant is after it walks 1 unit (let’s suppose the distance units are inches) along a curve r(t), assuming it starts at r(1).
Thinking of this in terms of arc length, the question gives you an arc length and a lower bound for integration, but the upper bound isn’t known. But you can use the arc length integral to find an equation you can solve for the upper bound:
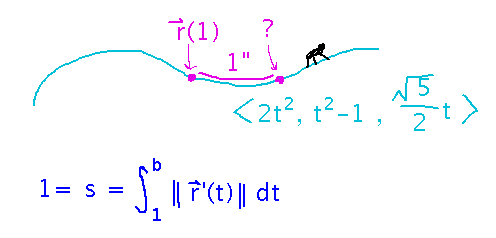
Once you have the upper bound, plug it in as the t value in r(t).
Plotting Multivariable Functions with Mathematica
The ContourPlot function plots level curves. Use ContourPlot3D for level surfaces.
Here are some examples.
Key Points
Mathematica can plot level curves or surfaces
The functions for doing so.
Limits
Section 4.2.
Definitions
δ-Disk
Draw a 2-disk around (1,0). Since a δ-disk is just a circle of radius δ, just draw such a circle centered at (1,0):
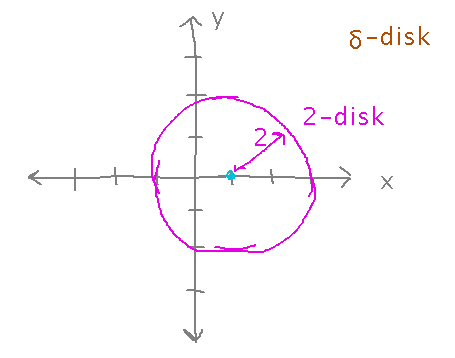
Other questions? What are δ-disks good for?
They are the 2-variable (and their more general form, δ-balls, are the more-than-2-variable) analogs of the single-variable idea of defining a limit partly in terms of an interval around a certain value of x. The single-variable limit definition requires that you can always keep f(x) as close as you want to a limit value L by keeping x within a certain distance of value a. With 2 variables, that “certain distance” means staying within a small circle around a point (a,b):
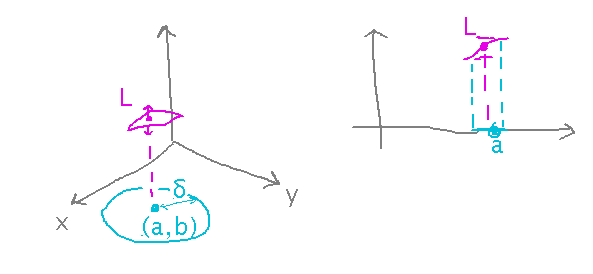
Finding Limits
2 Variables
Find lim(x,y)→(1,2)((x+y)/(3xy))2
You can find such limits much as you would with a single variable, namely by plugging in the actual values of x and y (thanks to the limit laws).

Key Points
Definition of multivariable limit.
Finding multivariable limits.
Next
When limits of multivariable functions don’t exist.
Then start talking about partial derivatives.
Read section 4.3.