SUNY Geneseo Department of Mathematics

Review for Exam 1

Thursday, October 4

Math 223 01
Fall 2018
Prof. Doug Baldwin

Misc

AWM Interest Meeting

Geneseo’s chapter of the Association for Women Mathematicians (AWM) is holding an interest meeting re becoming an official college student organization.

Wednesday, October 10th, 2:30; MacVittie Union room 324.

First Hour Exam

Friday, October 5, in class.

Covers material since the beginning of the semester (e.g., 3D space; lines, planes, and other surfaces; rectangular, polar, and cylindrical coordinates; vectors and their operations; vector valued functions and their calculus). Arc length and curvature may appear, but will probably be to some extent deferred to a future exam.

3 to 5 short-answer questions.

You’ll have the full 50-minute class period.

Open book, notes, computer as a reference or calculator; closed person.

Sample exam and solution are now available.

Review Sample Questions for Exam

See the sample exam and its solutions for details of questions and more formal descriptions of my solutions.

Sample Exam Question 3

Given a description of a cylinder (in the formal mathematical sense of the word), find a point on said cylinder.

Visualizing the cylinder, particularly the curve and lines parts, may help see how to set this up.

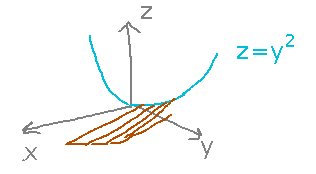
Parallel lines cutting across a parabola in the yz plane

Now use the parametric equation for a line to find conditions all points on the cylinder satisfy. Take the point(s) you need from the curve, and use the vector to give the direction:

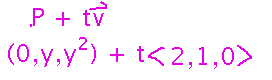
P + tv becomes (0,y,y^2) + t(2,1,0)

Finally, all you need is any point that is of this form, so simply pick y and t values that are easy to work with (and don’t result in x = 0), and plug them in. For example, y = t = 1:

y=1 and t=1 produce point (2,2,1)

Sample Exam Question 2

Specifically, finding the constant of integration.

Start with the knowledge that velocity is the integral of acceleration to find velocity. It has an unknown constant of integration, C:

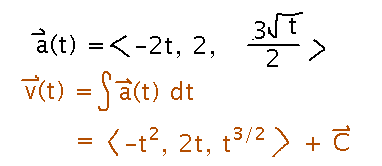
Integrate acceleration to get velocity plus a constant vector

To find that constant, you know what v(0) has to be, so plug 0 in for t in the velocity equation and solve for C:

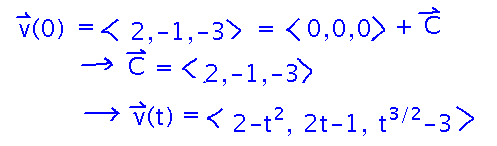
v(0) = (0,0,0) + C means C has to be (2,-1,-3)

Now to answer the question as asked on the exam, see if there’s a t value that simultaneously makes all 3 components equal to 0. It turns out there isn’t, each is 0 at a different t value (though you can stop as soon as you show that 2 of the components have different t values at which they’re 0).

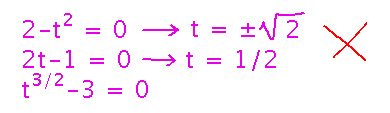
Each component is 0 at a different t value

Sample Exam Question 5

How many planes it takes to cover a set of points.

Imagine sliding a plane along the given normal vector. At certain places, one or more of the points will lie in the plane. Multiple points may or may not lie in the plane at the same time. The number of distinct planes you need in order to hit all the points is the answer to the question.

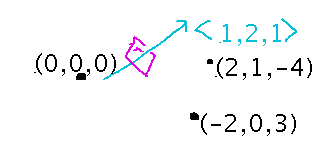
Plane along normal vector and 3 points

To figure out how many planes you need, set up a plane equation of the form Ax + By + Cz = D, recalling that A, B, and C come from the components of the plane’s normal, which you’re given, and plug the different points in to see what D values you get. Each different D corresponds to a different plane equation.

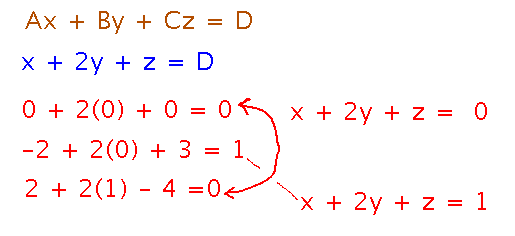
2 points produce 0 in plane equation, the other produces 1

Since 2 of the points produce the same D, you only need 2 planes.

Sample Exam Question 4

The dust mote (or speck) in a tornado.

Tornado carrying a speck of dust, and equation for speck's position

Realizing that the tangent to r(t), i.e., r′(t), points in the direction of “instantaneous motion,” you can answer this question by finding the derivative of r and evaluating it at t = 0:

Derivative of position is (2,0,10) when t=0

Purists might prefer a unit vector to specify a direction, but once you have r′(0), you can find the corresponding unit vector by dividing by its magnitude:

Unit vector is reciprocal of magnitude of derivative times derivative, or 1/sqrt(104) times (2,0,10)

(See the other solution document for a slightly simpler form of this unit vector.)

Sample Exam Question 1

Distance an airplane moves in 5 seconds given movement in 1 second.

Since the plane’s velocity doesn’t change, multiply the change in position per second by 5 to get the change in 5 seconds:

5 times (500,-200,100) is (2500,-1000,500)

Problem Set Question about Cylindrical Coordinates

What is the equation of a certain paraboloid in cylindrical rather than rectangular coordinates?

Compare the rectangular coordinate form of the paraboloid to equations relating rectangular to cylindrical coordinates, and notice that the right-hand side of the rectangular coordinate equation is just the square of the cylindrical radius. The left-hand side, z, is the same in both systems:

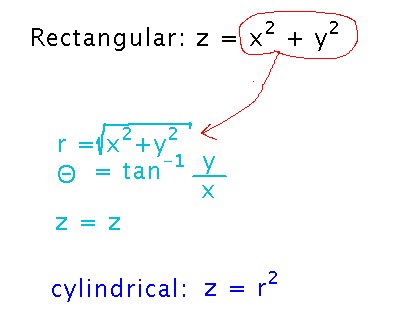
z = x^2 + y^2 becomes z = r^2 since r = sqrt(x^2+y^2)

(After exam and break.)

Introduction to multivariable functions.

In class, we’ll look at expressing some common formulas as multivariable functions, level curves, plotting with Mathematica, and coming up with multivariable functions that produce desired shapes when plotted.

Be prepared (or as prepared as the textbook gets you, things like Mathematica aren’t covered in it) to work with these ideas when you come to class, and bring a computer.

Next Lecture