Misc
Actuary Interest Meeting
Today, 3:00 - 4:00, South 328
Learn what an actuary is and meet the actuary club
First Hour Exam
Friday, October 5, in class.
Covers material since the beginning of the semester (e.g., 3D space; lines, planes, and other surfaces; rectangular, polar, and cylindrical coordinates; vectors and their operations; vector valued functions and their calculus). Arc length and curvature may appear, but will probably be to some extent deferred to a future exam.
3 to 5 short-answer questions.
You’ll have the full 50-minute class period.
Open book, notes, computer as a reference or calculator; closed person.
Sample exam and solution are now available.
Questions?
The Principal Unit Normal
Calculation
Find the principal unit normal to r(t) = 〈 -sin t, cos t, √3 t 〉.
The principal unit normal is the derivative of the unit tangent vector, scaled to unit length. So the basic calculation involves computing and scaling 2 derivatives.
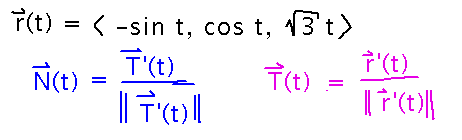
Calculate the unit tangent vector by differentiating and scaling r:
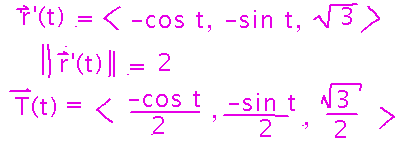
Then calculate the principal unit normal by differentiating and scaling T:
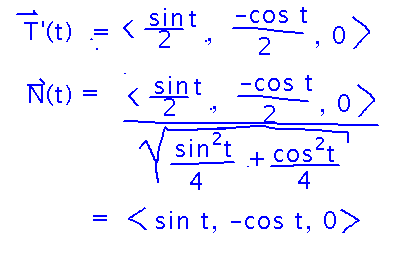
Physical Significance
What’s the geometric relationship between a constant-magnitude vector and its derivative? Figure it out by starting with an expression for magnitude (or at least its square), then take derivatives:

They’re perpendicular!
So the principal unit normal is always perpendicular to the tangent vector. Furthermore, because the principal unit normal is a derivative, it points in the direction the tangent is changing towards, i.e., the direction the curve is turning.
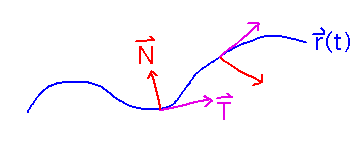
This particularly has implications for velocity and acceleration vectors: You can decompose acceleration into a component parallel to the tangent, which is the portion of acceleration responsible solely for speeding up or slowing down the object (since the tangent vector is parallel to velocity), and a component parallel to the principal unit normal, which is solely responsible for changing the object’s direction.
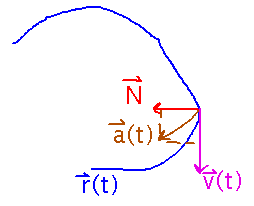
Key Points
Principle unit normal as a vector that gives direction towards which a curve turns.
Formula for the principal unit normal.
Next
Multivariable functions.
Read section 4.1.