SUNY Geneseo Department of Mathematics

Introduction to Multivariable Functions

Wednesday, October 10

Math 223 01
Fall 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Questions?

Multivariable Functions

Section 4.1.

Examples

A function of 2 variables that calculates their average.

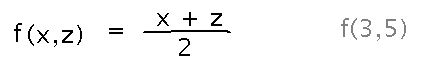
f(x,z) = (x+z) / 2; f(3,5) calculates average of 3 and 5

Multivariable functions look a lot like single-variable ones, they just introduce more variables to represent the inputs. Applying those functions to concrete arguments also looks a lot like the single-variable case, but with more arguments.

A function of 2 variables, the lengths of the legs of a right triangle, that calculates the length of the hypotenuse.

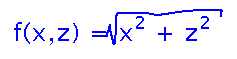
f(x,z) = sqrt( x^2 + z^2 )

A function of 3 variables representing the width, height, and depth of a box that calculates the volume of the box.

f(x,y,z) = xyz

Multivariable function definitions scale up to more variables in the natural way.

A function of 6 variables, the coordinates of 2 points in space, that calculates the distance between the points.

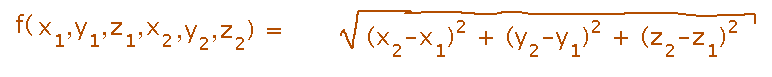
f(x1,y1,z1,x2,y2,z2) = sqrt((x2-x1)^2+(y2-y1)^2+(z2-z1)^2)

Multivariable functions can have many variables, and they can be named in all the ways other variables are (e.g, with subscripts).

Sturges Auditorium

Field trip? Unfortunately, not available now. But imagine a large room shaped like a large tunnel that extends along the x axis.

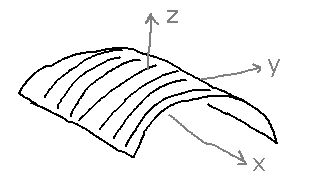
Semicircular tunnel with a coordinate system at the center

Level curves

A level curve is a path in the xy plane along which f(x,y) doesn’t change.

So in this example, any straight line parallel to the x axis is a level curve.

Equations for the Ceiling

Suppose the room is 40 feet long (-20 ≤ x ≤ 20), 20 feet wide (-10 ≤ y ≤ 10), 20 feet high (0 ≤ z ≤ 20).

Assume the cross-section of the room is roughly a semicircle. The equation of a semicircle can be derived from that for a circle:

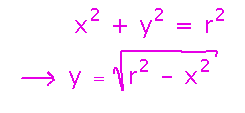
x^2+y^2 = r^2 implies y = sqrt(r^2-x^2)

This provides an equation for the ceiling’s height in terms of y, by using the auditorium’s height as the radius, and scaling y so the height goes to 0 when y = ±10. Notice that x doesn’t play a role in determining height (z), but nonetheless defines bounds for the room. You can still think of height as a function of x and y.

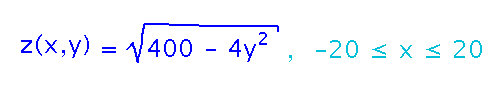
z(x,y) = sqrt( 400 - 4y^2 ) for x between -20 and 20

(This is more an elliptical cross section than a perfectly circular one, but that’s OK.)

Plotting with Mathematica

The Plot3D function plots a 2-variable function. Here’s an example plotting the auditorium from above.

Key Points

What multivariable functions look like.

The concept of a level curve.

Plotting multivariable functions.

Next

First, a little more about plotting, particularly level curves and level surfaces.

Then limits of multivariable functions.

Especially finding limits and determining when they don’t exist.

Read section 4.2.

Next Lecture