SUNY Geneseo Department of Mathematics

Curvature

Monday, October 1

Math 223 01
Fall 2018
Prof. Doug Baldwin

Misc

First Hour Exam

Friday, October 5, in class.

Covers material since the beginning of the semester (e.g., 3D space; lines, planes, and other surfaces; rectangular, polar, and cylindrical coordinates; vectors and their operations; vector valued functions and their calculus). Arc length and curvature may appear, but will probably be to some extent deferred to a future exam.

3 to 5 short-answer questions.

You’ll have the full 50-minute class period.

Open book, notes, computer as a reference or calculator; closed person.

I’ll make a sample exam available.

Questions?

Can I extend the due date for Problem set 5? Yes, grade-by date is now Thursday Oct. 11.

Arc Length Parameterization

Friday we started finding an arc length parameterization for the curve r(t) = 〈 t², t², t² 〉which is a straight line, but one in which distance from the origin changes faster as t gets larger. The first step was to find the arc length function. Now we need to use it as an equation for s in terms of t, and rearrange that equation to get t in terms of s:

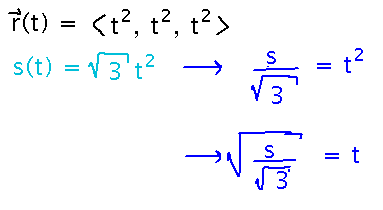
For r(t) = (t^2,t^2,t^2), s(t) = sqrt(3) t^2

Then we can substitute that result for t in the original parameterization to get a parameterization in terms of distance from the origin (or some other reference point), i.e., a parameterization in terms of arc length.

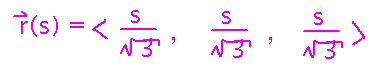
r(s) = ( s/sqrt(3), s/sqrt(3), s/sqrt(3) )

Curvature

The last two subsections of section 3.3.

Find Curvature

Example: r(t) = 〈 e^2t, 3e^2t, e^2t-1 〉. Try using the formula involving cross products of derivatives of r:

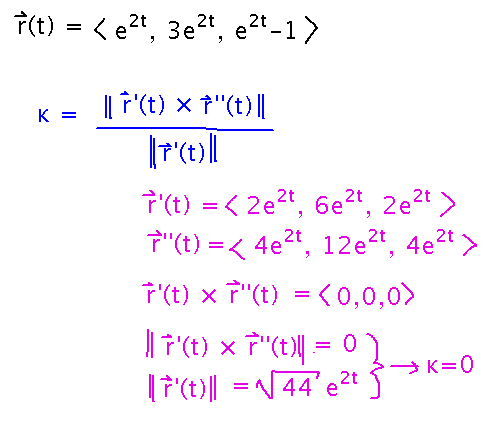
Curvature = magnitude of cross product of r's 1st & 2nd derivatives over magnitude of derivative

A curvature of 0 means that this “curve” is a straight line. Reparameterizing by making the common e^2t a variable makes this clearer:

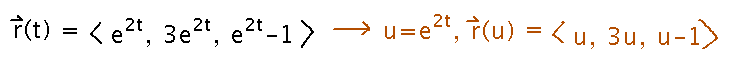
Setting u = e^(2t) makes r(u) = ( u, 3u, u-1 )

Can Mathematica find curvature for you? It turns out it can, a short Google search uncovers the ArcCurvature function. Here’s an example notebook.

There are other formulas for curvature, one that I find interesting being in terms of the unit tangent vector and the derivative of r. You can analyze the r(t) = 〈 e^2t, 3e^2t, e^2t-1 〉curve using it like so...

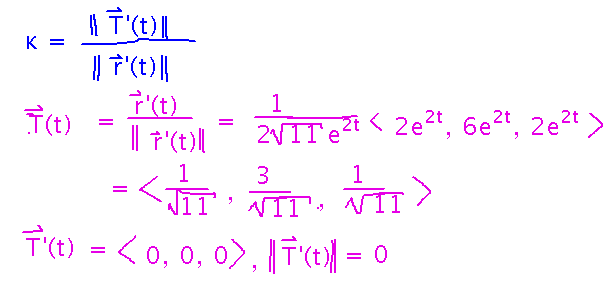
Curvature = magnitude of T-prime over magnitude of r-prime; magnitude of T-prime is 0

The principal unit normal vector.

See (you should already have read) “The Normal and Binormal Vectors” in section 3.3.

Next Lecture