More about Arc Length

Return to Course Outline

Previous Lecture

Misc

First Hour Exam

Next Friday, October 5, in class.

Covers material since the beginning of the semester (e.g., 3D space; lines, planes, and other surfaces; rectangular, polar, and cylindrical coordinates; vectors and their operations; vector valued functions and their calculus). Arc length and curvature may appear, but will probably be to some extent deferred to a future exam.

3 to 5 short-answer questions.

You’ll have the full 50-minute class period.

Open book, notes, computer as a reference or calculator; closed person.

I’ll make a sample exam available.

Questions?

Arc Length

Calculating It With Software

Find the length of the curve r(t) = 〈 t²+1, 2t², t 〉between t = 0 and t = 2.

The obvious way to do this is to set up the arc length integral according to the formula from last class, and then use Integrate to integrate it. By default, Mathematica produces symbolic results, which in this case involves an inverse hyperbolic sine function that’s not particularly intuitive. Use the N function to see the result as a decimal number instead of symbolically. And finally, notice that Mathematica has a built-in ArcLength function which saves you having to set up the integral by hand.

Here is the notebook demonstrating all of these things.

Arc Length Parameterization

What’s the point?

Parameter corresponds exactly to length along the curve from some reference point. Notice that this doesn’t have to be the case for parametric curves: equal changes in the parameter value can produce points that are not equally spaced along the curve:

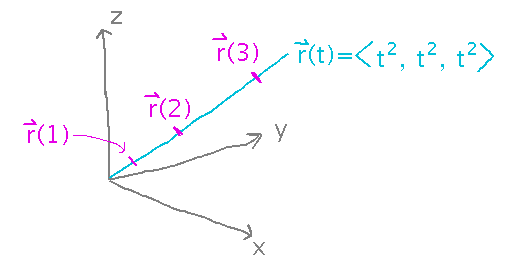
Find the arc length parameterization for r(t) =〈 t², t², t² 〉

The first step is to find the arc length function (which we’ll do using t = 0 as the reference):

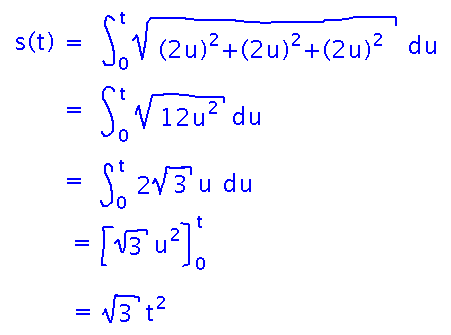
This function can be interpreted as an equation for distance along curve as a function of t. Solving it for t in terms of s gives something you can replace t with in the original parameterization to produce a parameterization in terms of distance. We’ll do that for this example first thing Monday.

Problem Set

See handout for details.

Next

Also Monday, after we finish arc length parameterization.

Curvature

Read the

• Curvature
• The Normal and Binormal Vectors

subsections of section 3.3.

Next Lecture