SUNY Geneseo Department of Mathematics

Introduction to Arc Length

Thursday, September 27

Math 223 01
Fall 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Questions?

Arc Length

First subsections of section 3.3.

Formula

Where does the formula for arc length come from?

You can’t just use the distance formula between points r(a) and r(b), because the distance formula gives straight-line distance but the curve probably isn’t straight between those points. But if you approximate the curve as a sequence of more and more short straight lines, the approximation comes closer to the curve as the number of lines grows, and you can use the distance formula on each line. So arc length is a Riemann sum of distance formula applications, which becomes the integral in the formula.

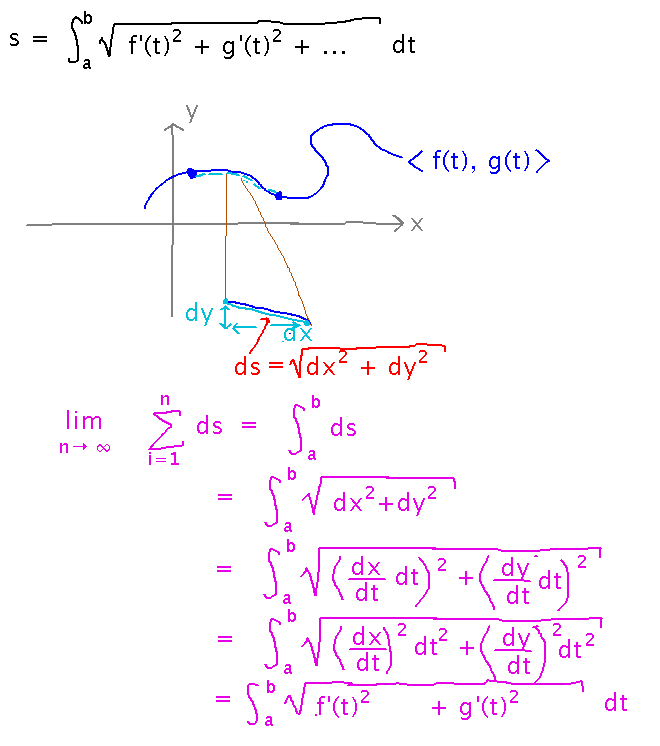
Curve approximated by many short lines each of length sqrt( dx^2 + dy^2 )

Practice

By Hand

What is the length of the curve r(t) =〈 sin(2t), 3t, cos(2t) 〉between t = 0 and t = 1?

Plug r(t) into the arc length formula (noting a convenient sin2 + cos2 that becomes 1)...

Find r prime, then use its components in magnitude formula and integrate

What is the corresponding arc length function, measuring from t = 0?

The arc length function is just a function that gives the arc length from some reference point to any other point along the curve, as a function of the t parameter.

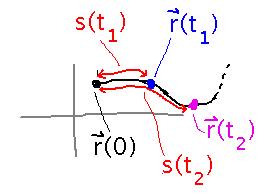
Curve with r(t_1) and r(t_2) points and distances s(t_1) and s(t_2) to them

So find the arc length function much as you find a single arc length, but with the upper bound on the integration being the function’s argument.

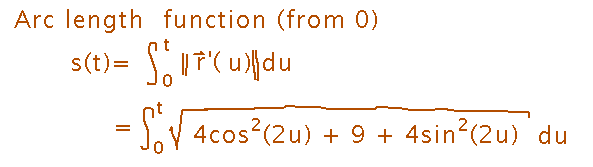
Integrate magnitude of derivative of position, with upper bound t

Key Points

The arc length formula comes from the distance formula applied to infinitely many infinitesimally short line segments.

Using the arc length formula to find lengths.

Arc length functions.

Next

Arc length with Mathematica.

Arc length parameterization.

Next Lecture