SUNY Geneseo Department of Mathematics

Lines in 3 Dimensions

Thursday, September 13

Math 223 01
Fall 2018
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Questions?

Lines in Space

First part of section 2.5.

Equations

Find an equation for the line through (1,2,1) in direction 〈 1, 1, -3 〉

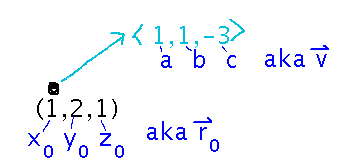
A point at (1,2,1) with a direction vector (1,1,-3)

One form of equation is the “symmetric equations,” which assert that certain expressions in x, y, and z must all be equal:

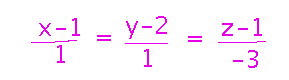
(x-1)/1 = (y-2)/1 = (z-1)/(-3)

The symmetric equations come from the parametric equation for the line, which expresses the line as a vector with a parameter (t):

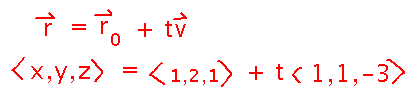
Vector (x,y,z) = (1,2,1) + t(1,1,-3)

Ray Tracing

A technique for producing hyper-realistic computer-generated images, based on modeling what happens to individual rays of light on their way to a viewer (although computationally, ray tracing traces the rays backwards from the eye into a virtual scene).

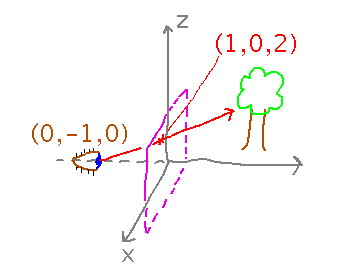
Eye on -y axis sends rays into virtual scene through window on xz plane

Those rays are just parametric lines, defined by 2 points: the eye position and a point in the window. So, for example, find an equation for the line through points (0,-1,0) and (1,0,2).

Use the difference between the points as the direction vector, and either point as the r0 reference.

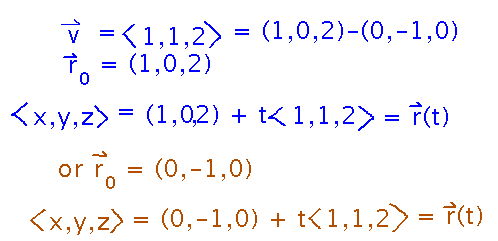
Equations for lines with direction (1,1,2) through either (1,0,2) or (0,-1,0)

Where does that line intersect the plane y = 3?

Set the y component of either parametric equation equal to 3, then solve for t. Plug t into the whole parametric equation to get the actual intersection point. Note that both equations give the same point, just at different t values -- both equations are describing the same line.

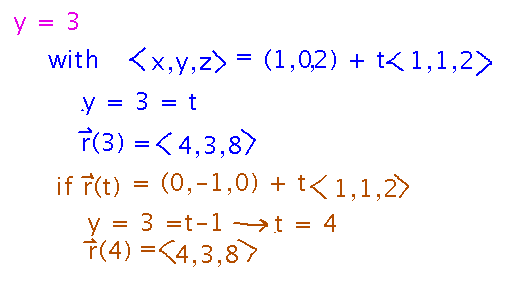
Two line equations solved for t when y = 3

How about the plane y + z = -4? Is the intersection point visible to the “eye”?

Plug the parametric equations for y and z into the plane’s equation, to get an equation in only 1 variable. Then solve for t, and plug back into the parametric equation if desired, as before. If you pick the eye’s position (i.e., (0,-1,0) here) as the reference point for the line, negative t values correspond to positions behind the eye and thus invisible, while positive t values correspond to positions in front of the eye and so potentially visible.

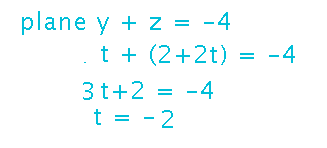
x + y = -4 becomes t + 2 + 2t = -4, or t = -2

Key Points

Equations (symmetric and parametric) for lines.

Using the equations to find intersections.

Problem Set

On lines, planes, and cross product, and other vector operations indirectly.

See handout for details.

Next

More lines.

Next Lecture