Questions?
Reasoning about Lines
Still from the first part of section 2.5.
Intersections between Lines
Do lines L(t) = (0,1,0) + t〈1,1,1〉 and M(t) = (2,0,1) + t〈0,3,1〉intersect? If so, where?
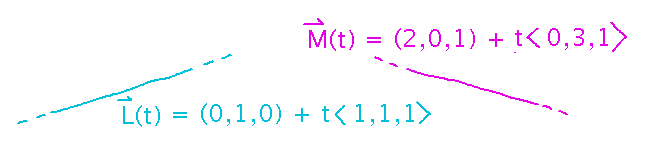
The key strategy is to see if there is any way to make the x, y, and z components of both lines equal, when each line has its own parameter (to ensure that the lines simply have to cross, not meet at the same parameter value). Doing that produces a system of equations you can solve for the parameters. Plugging the solutions back into their corresponding line equations gives the coordinates of the intersection:
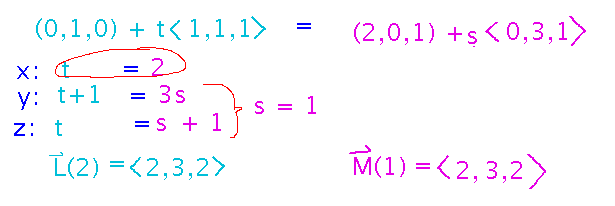
What if you raise L(t) 1 unit in the z direction? What does its equation become, and do the lines intersect?
The new equation just has 1 in the z component of the point. The point part of a line’s equation is what gives the line its position.
Now set up and solve a system of equations as before, but this time the system doesn’t have a solution, meaning that the lines don’t intersect.
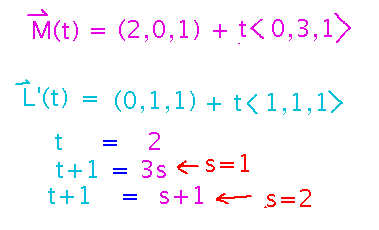
Lines as Vectors
How come I identify the values of these functions, e.g., L(t), as vectors not points? Geometrically they ought to be points, which are geometrically not the same as vectors, but I’ve identified the functions as producing vectors (that’s what the bold face name in typed text, or the arrow over it in handwritten text, means) and so I’m being consistent with that identification in writing their results. Identifying them as producing vectors is in turn how we’ll look at functions in a few days.
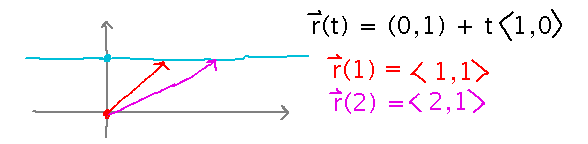
More generally, vector functions are often considered to define a line or curve in space thanks to a way of equating vectors and points: think of a vector as representing the point you get to by adding that vector to the origin. For example, consider 2D line r(t) = (0,1) + t〈1,0〉 (notice that parametric equations for lines work in any number of dimensions). When you draw this line, it’s horizontal, but the vectors r(t) run diagonally from the origin to the points on the line.
Distance
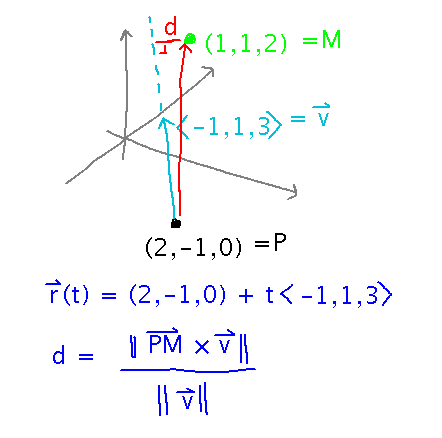
Intrepid but not very competent space-traveler Spacey is fleeing the evil Zrg space station at galactic coordinates (2,-1,0), heading for planet G’nseo at (1,1,2). Spacey gets the direction to G’nseo wrong, heading in direction 〈-1,1,3〉. What is the closest to G’nseo that Spacey actually gets?
Spacey’s closest distance is the length of a line segment from G’nseo to Spacey’s path and perpendicular to that path. Thus the path, that line segment, and a line from any point on the path (P) to G’nseo (M) define a right triangle, in such a way that the length of the line segment (i.e., the distance from G’nseo to Spacey’s path) is the length of the PM line times the sine of the angle between it and Spacey’s path. Vector cross products can be used to find sines, leading to the standard equation for the distance from a line to a point:
Next
Planes.
Read the...
- Equations for a Plane
- Parallel and Intersecting Planes
subsections of section 2.5