Misc
Colloquium
Two students talking about research they did here this past summer.
BethAnna Jones, “This is Your Brain on Math: The Mathematics of Tracking Neurons”
Eric Piato, “Exploring Graph Theory: Preliminaries, Algebra, and the Eigenvalues of Anti-Regular Graphs”
Eric’s talk is about “graphs” in the sense of networks of objects with relations between them, not in the sense of plots of functions.
Both Tuesday, Sept. 18 at 4:00 PM, Newton 203.
Extra credit for going and writing ca. 1 paragraph on connections you make to one or both talks or reactions you have to them.
Review Sessions
Calculus 1, South 340, 2:30 - 3:20 today (Sept. 12)
Trigonometry, South 338, 2:30 - 3:20 today
Run by MLC tutors
Questions?
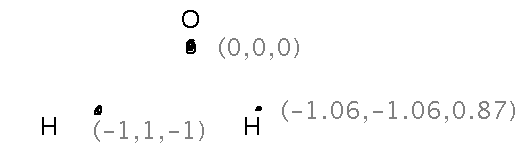
Are the coordinates in problem set question 6 (about atoms in a water molecule) points or vectors? They are points, but can quickly be turned into vectors if that helps.
Cross Products
Section 2.4.
Basic Idea
Calculate 〈 1, -2, 1 〉 × 〈 3, 1, 2 〉
The cross product has a somewhat hard-to-remember formula. I remember it as differences of products that “cross” between the vectors, each component of the product being computed from the other components of the original vectors.

There’s also a mnemonic based on determinants, if you’re comfortable with them, and minimally you just need to remember that “×” means something special with vectors that you can look up.
Plugging the above vectors’ components into the cross product formula, however you remember it, gives…

Applications
Torque
Why do mechanics push/pull wrenches at a 90º angle to the handle?
Because torque (twisting force) is a cross product, and the magnitude of a cross product depends on the sine of the angle between the vectors. A 90º angle produces the largest possible value of sine.
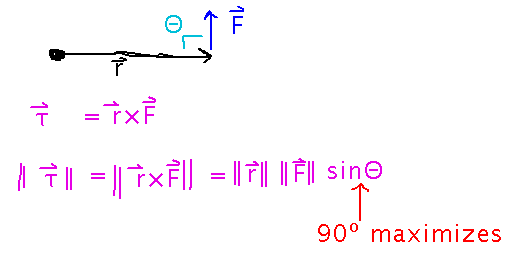
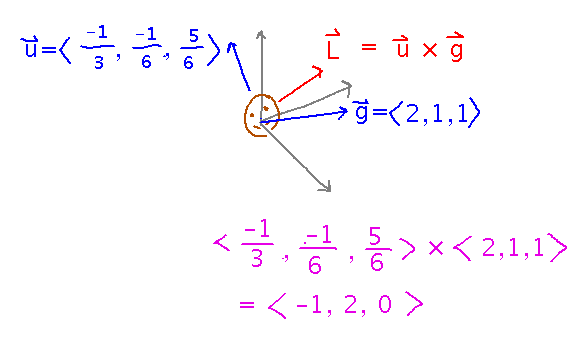
Perpendicular Vectors 1
Our video game character from last class with gaze vector 〈 2, 1, 1 〉has an “up” vector of 〈 -1/3, -1/6, 5/6 〉. Find a vector that they see as pointing to their left.
The cross product of the gaze and up vectors will be perpendicular to both and so pointing left or right. Use the right hand rule to decide what order to do the cross product in to get a result pointing left.
Perpendicular Vectors 2
Computer graphics programs generally represent curved surfaces (e.g., the animated snake’s body or head) as meshes of small triangles. They also need vectors perpendicular, or “normal” to these triangles in order to calculate how light reflects from them.
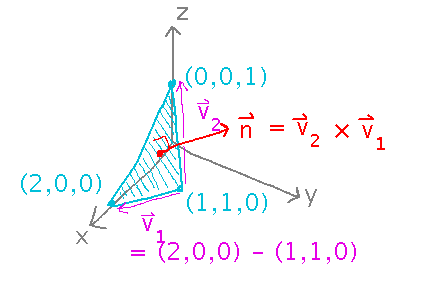
Suppose a triangular patch of some object has corners (2,0,0), (1,1,0), and (0,0,1). Find a normal vector to this triangle that points more away from than towards the origin.
Once again, use the cross product. In particular, the cross product of any two vectors in the plane of the triangle will be perpendicular to that triangle. Vectors along two edges of the triangle are convenient choices.
Key Points
What the cross product is and the formula for it.
The magnitude of the cross product and its relation to angle.
Geometric significance of the cross product and its applications.
Next
Equations for and relationships between lines in 3 dimensions.
Read subsections
- Equations for a Line in Space
- Distance between a Point and a Line
- Relationships between Lines
of section 2.5 in the textbook.