SUNY Geneseo Department of Mathematics
Monday, September 10
Math 223 01
Fall 2018
Prof. Doug Baldwin
Calculate 〈 3, 1, -2 〉•〈 2, -2, 1 〉
〈 3, 1, -2 〉•〈 2, -2, 1 〉 = (3)(2) + (1)(-2) + (-2)(1) = 2
Prove that dot product distributes over vector addition, i.e., that u • (v + w) = u • v + u • w
(Property 2 in Theorem 2.3)
The basic idea, as in many proofs about algebraic properties of vectors, is to break the vectors down into sequences of numbers, apply the definitions of the vector operations to the numbers (where you know the algebra well), and finally reassemble the results into vectors:
A character in a video game has gaze vector 〈 2, 1, 1 〉.
What is the angle between this vector and the x axis?
Use the equation for the cosine of the angle between two vectors. One of the vectors is the gaze vector, but what’s the other? It can be any vector parallel to the x axis, since all such vectors make the same angle with the gaze vector.〈 1, 0, 0 〉is a good choice because it has magnitude 1 and is easy to calculate dot products with.
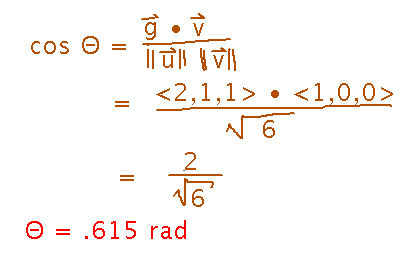
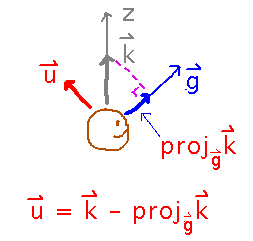
Assuming the character isn’t rolling their head, find a plausible “up” vector.
If the character isn’t rolling their head side to side, then “up” points more or less in the direction of the global z axis. So take “up” to be the component of a unit vector in the z direction (i.e., standard unit vector k = 〈 0, 0, 1 〉) that is perpendicular to the gaze vector. You can find this by subtracting the projection on k onto the gaze vector from k.
The basic definition of dot product.
Proof style for vector algebra.
Using dot product to find angles, projections.
On vectors in general, with a little bit about cylindrical coordinates.
See handout for details.
The cross product.
Read section 2.4.