SUNY Geneseo Department of Mathematics
Friday, September 7
Math 223 01
Fall 2018
Prof. Doug Baldwin
Wolfram is offering a free online training course for Mathematica.
If interested, register at http://url.wolfram.com/8Ws2VAs/
Probably covers more than we will use in this course, and isn’t coordinated with it, but maybe interesting.
“GROW STEM” = “Geneseo Reaching Out to Women and Under-Represented Groups in STEM Fields”
Mixer for anyone interested.
Wednesday, Sept. 12, 5:30, ISC 115.
Find the “average” of 〈 1, 3, 1 〉, 〈 3, 2, 0 〉, and 〈 -1, 1, 2 〉
That average works much like an average of scalars does, i.e., add the vectors together and divide by the number of vectors. But vector addition isn’t quite the same as scalar addition, and “division” is expressed as scalar multiplication by a fraction.
How about a unit vector that points in the same direction as that average?
To find the unit vector, divide by the vector’s magnitude, i.e., compute a scalar product of the vector with the reciprocal of its magnitude.
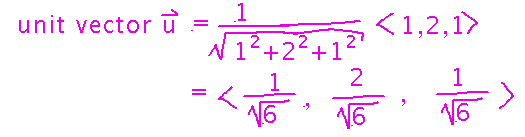
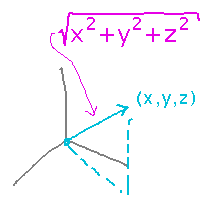
Magnitude is geometrically the length of the vector, and so the formula for it follows from the distance formula or Pythagorean Theorem.
A moving object with mass m and velocity v has momentum p = mv.
The total momentum of a set of objects remains constant as long as no external forces act on those objects.
Suppose objects with masses m1 = 2g and m2 = 4g and velocities v1 = 〈 1, -1, 2 〉cm/sec and v2 = 〈 1, 2, 2 〉 cm/sec collide. After the collision v1′ = 〈 1, 1, 1 〉cm/sec.
What direction is object 2 moving in after the collision?
Calculate momenta before and after (at least where velocity is given) the collision using the p = mv formula. Then set the sum of the momenta before the collision equal to the sum after and solve for the unknown momentum (vectors have algebraic rules very similar to scalars). The final momentum gives the direction, although you could scale it to a velocity or even a unit vector if you wanted.
What if these are space-time objects with v1 = 〈 1, -1, 2, 2 〉cm/sec and v2 = 〈 1, 2, 2, -1 〉 cm/sec?
Rules for vector addition and scalar multiplication scale up to any number of dimensions, so you’d solve this problem in essentially the same way as the 3D one. (Though I don’t know if there’s a physically meaningful 4-dimensional version of momentum.)
(i.e., Example 2.20)
Is it utter nonsense that the units in that example start in yards and end in miles per hour?
No, it makes sense that you can use distances in yards to calculate the direction of a vector, and then multiply that vector by an appropriate scale factor to turn it into a velocity in the same direction. The scale factor has a conversion between units built in.
Vector addition, scalar multiplication.
Vector magnitude aka length.
Unit vectors.
The dot product.
Read section 2.3.