Area Between Curves

Misc

Review Session

Thursday, May 9 (study day)

1:00 - 2:00

In our regular classroom (Sturges 221).

Bring things you want to talk about.

SI

Review on Wednesday, 4:00 - 7:00, Bailey 209.

Final Exam

Thursday, May 16, 12:00 Noon.

In our regular room.

Comprehensive, but emphasizing material since the 2nd hour exam (e.g., Mean Value Theorem, limits at infinity, Riemann sums, definite integrals, substitution, applications of integration; roughly problem sets 7 through 9).

Rules and format otherwise similar to hour exams, especially open-references rule.

Designed for about 2 hours, you’ll have 3 hours 20 minutes

Practice questions are now available in Canvas.

I’ll bring donuts and cider.

SOFIs

SOFIs are under way.

8 responses (26%) so far. Thank you!

But please keep filling them out. I do read them and apply the feedback where possible to future classes (like the mid-semester feedback).

MLC

Extended hours during study day and finals.

Questions?

Extended Power Rule

How to approach question 5 on the problem set (prove an antiderivative power rule for integrands of the form (x+k)ⁿ for constants k).

There are two ways you might approach this: one is to use a u-substitution to find the antiderivative, the other is to differentiate the proposed antiderivative and check that the result equals the original integrand.

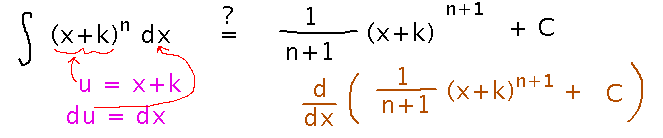
Pursuing the u-substitution approach shows that the proposed antiderivative is correct:

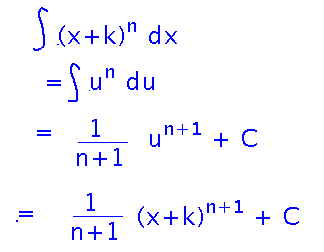
Here’s the complete analysis, as it looked when we finished it in class:

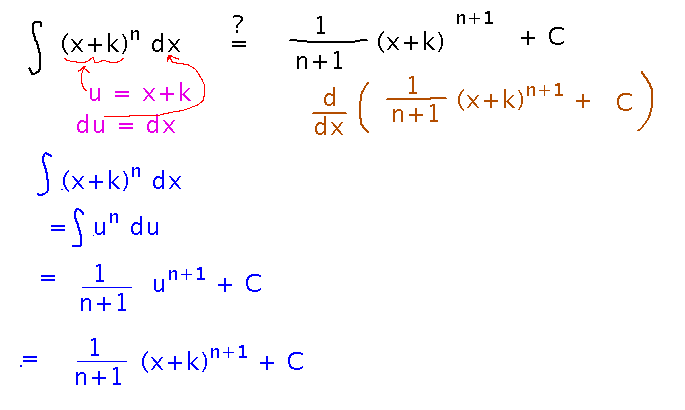
Integration in Mathematica

How to do it? Use the Integrate function. Here is a notebook with examples of both an indefinite integral (antiderivative) and a definite integral.

Area between Curves

Section 6.1.

Example

Friday we started thinking about the area of a (very geometric) pond whose edges are the graphs of y = x² and y = 4 - x². We realized that the area would be the integral of the difference of the functions.

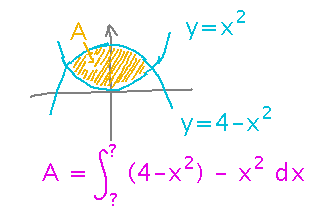
Now finish the problem.

The first step is to figure out where the boundary curves intersect, because the x values of the intersections will be the bounds of integration.

Now integrate as you would any other definite integral:

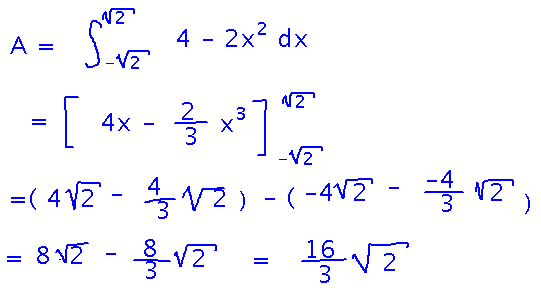
Here’s the complete solution, as it looked when we finished it in class:

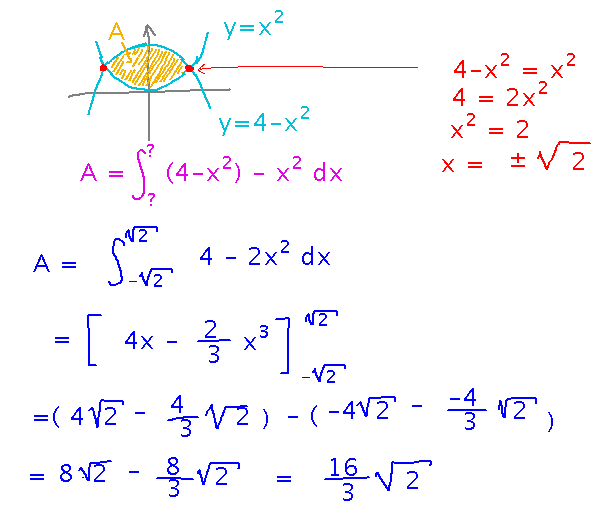
Key Points

Procedure for finding the area between f(x) and g(x), with f(x) ≥ g(x)

• Find where the functions intersect.
• Set up the integral of f(x) - g(x), using the x coordinates of the intersection points as bounds. If f(x) ≥ g(x) in some intervals but not others, set up separate integrals over each interval; use f(x) - g(x) where f(x) is bigger and g(x) - f(x) where g(x) is bigger.
• Integrate.

Volumes as Integrals of Slices

Section 6.2.

Example

Can you find the volume of this tapered prism as an integral?

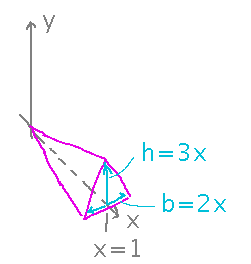
If not for the taper, you could just multiply the area of the triangular end by the length of the prism. So what if we concentrate on a thin slice of the prism, over which it doesn’t taper much?

Now the approximate volume of the whole prism is the sum of the (approximate) volumes of all the slices:

Look! This is a Riemann sum!

Finally (and not surprisingly, since we have a Riemann sum), we can get the exact volume by taking the limit as we approach an infinite number of infinitely thin slices. That limit, moreover, is an integral.

Here’s the whole analysis, as it looked when we finished it:

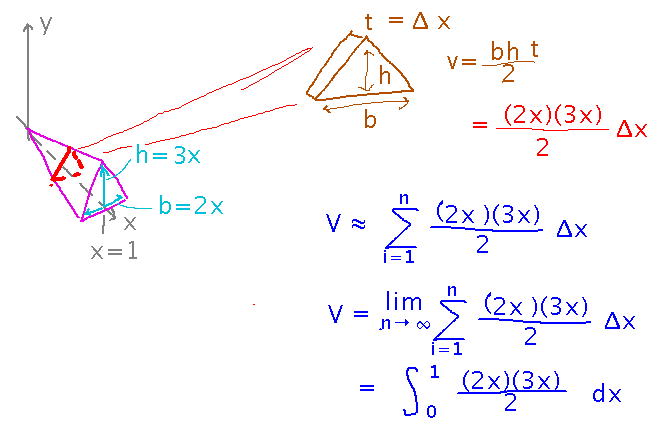
Key Point

Volumes of irregular shapes can sometimes be calculated as sums of volumes of thin slices, which in turn leads to an integration formula for them.

Next

More volume.

Read (or finish reading) section 6.2.