Volume by Slices

Return to Course Outline

Previous Lecture

Misc

Extended MLC Hours

9:00 AM to 3:30 PM weekdays through Wednesday of finals (added 1 to 1 1/2 hours front and back).

Evening hours unchanged (as far as I can see).

Reading Survey

For the math department assessment committee.

Visit https://forms.gle/rctWLa7Rxt19RHfj8 and fill out the form.

OR get a paper copy from me, fill it out, and return it to me.

Extra Credit

“Due” by the final exam.

SI

Review today, 4:00 - 7:00, Bailey 209.

Review Session

Tomorrow.

1:00 - 2:00

In our regular classroom (Sturges 221).

Bring things you want to talk about.

Final Exam

Thursday, May 16, 12:00 Noon.

In our regular room.

Comprehensive, but emphasizing material since the 2nd hour exam (e.g., Mean Value Theorem, limits at infinity, Riemann sums, definite integrals, substitution, applications of integration; roughly problem sets 7 through 9).

Rules and format otherwise similar to hour exams, especially open-references rule.

Designed for about 2 hours, you’ll have 3 hours 20 minutes

Practice questions are now available in Canvas.

I’ll bring donuts and cider.

SOFIs

SOFIs are under way.

11 responses (35%) so far. Thank you!

But please keep filling them out. I do read them and apply the feedback where possible to future classes (like the mid-semester feedback).

Questions?

Volume via Slices

Section 6.2.

Introductory Example

Last class we discovered that volumes of irregular shapes can (sometimes) be calculated as sums of volumes of thin slices, which leads to volume as a Riemann sum and thus as an integral:

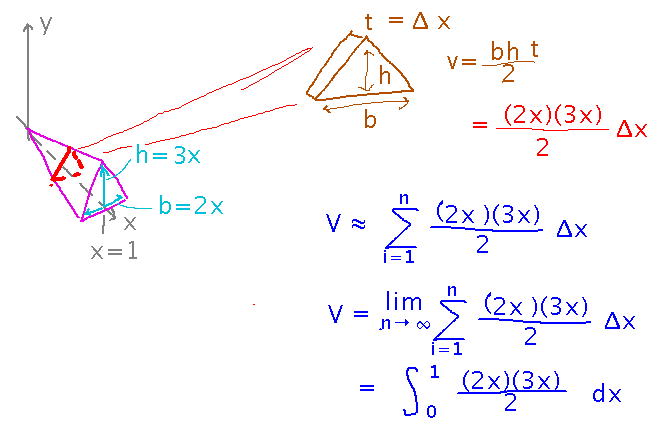
So what is the volume of that prism?

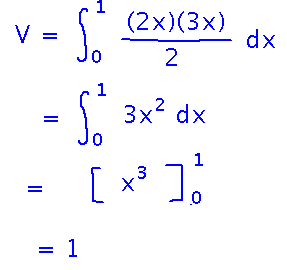
Side question: if the bounds of an integral reverse (i.e., upper bound has smaller numeric value than lower), do you have to do anything special to evaluate it? No, the “subtract antiderivative at lower bound from that at upper bound” rule takes care of it for you. For example...

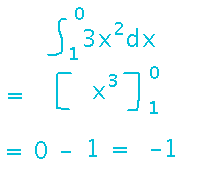
A Volume of Revolution

Suppose you take the region between the line y = x/2 and the x axis, from x = 0 to x = 2, and spin it around the x axis to form a cone. What is the volume of that cone?

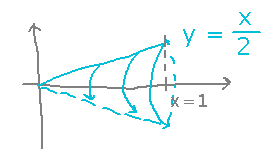
The area of a circle seems relevant, but how? Because thin slices of the cone have circular faces, and so their volumes are the areas of those circles times their thicknesses:

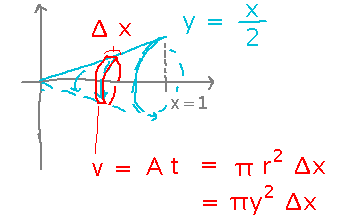
Now the approximate volume of the cone is a Riemann sum of volumes of thin slices, so the exact volume is an integral, which can be evaluated like any other definite integral:

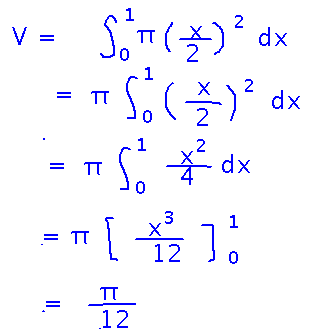
Here’s the complete volume calculation, as it looked when we finished it in class:

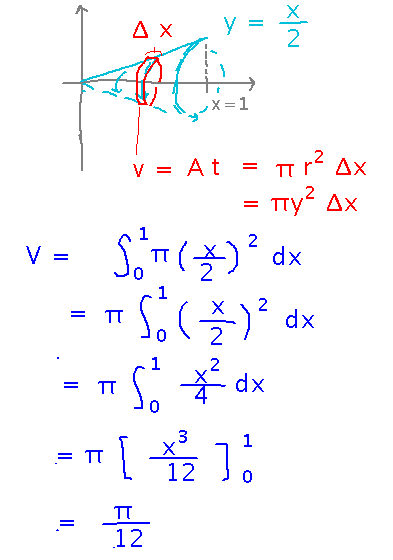
Rotation Around Other Axes

What if you rotate the line y = 3x, between x = 0 and x = 1, around the y axis to make a cone? What’s the volume of that cone?

The ideas are the same as above, except now it’s easiest to take slices perpendicular to the y axis, not the x. So re-express x in terms of y (since the x value will be the radius of the cone at any particular y), and figure out the range of y values the cone covers:

Now integrate with respect to y:

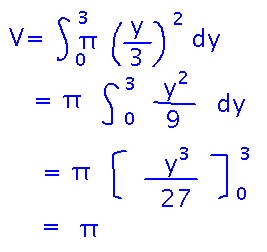
Here’s the complete picture and calculation, as they appeared when we finished:

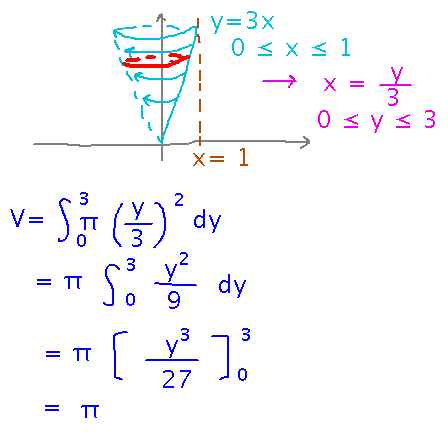
Key Points

To find a volume by slicing:

• Pick an axis to slice perpendicular to that will give you nice formulas for cross-sectional area
• Find the formula for the area of a face (e.g., triangle, circle) of a slice
• Volume of an infinitely thin slice has formula “A dx” where A is the area of a slice at x coordinate x (or y coordinate if integrating with respect to y).
• Integrating A dx over the range of x occupied by the shape gives volume

You can do this around any axis.

(No Next Lecture)