Definite Integrals, Part 1

Return to Course Outline

Previous Lecture

Questions?

Area and Definite Integrals

From Last Class

Use rectangles to estimate the area between the graph of y = x and the x axis between x = 1 and x = 3.

We figured out by geometric calculations on Monday that the exact area is 4 square units.

Here’s the idea of approximation with rectangles, using just 2 rectangles for demonstration:

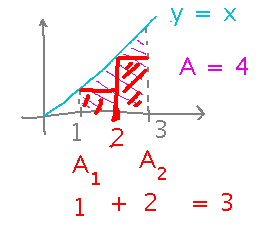
Both rectangles have width 1. The first rectangle goes from the x axis up to the line y = x at x = 1, so has height 1. The second rectangle goes up to the line at x = 2, so has height 2. The total area is the sum of the rectangle’s areas, or 1 + 2 = 3.

To get a more accurate area estimate, use more rectangles and make them thinner. But rather than calculate lots of areas by hand, and then add them up by hand, let’s try to find a general formula that gives the total area inside n rectangles.

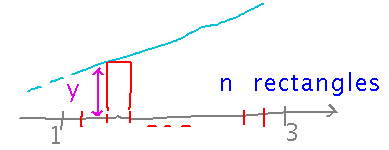
The first step is to figure out the width of each rectangle, Δx. It turns out to be just the total width of the interval from x = 1 to x = 3, divided by n rectangles:

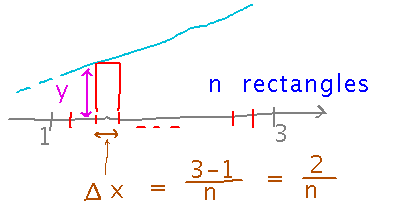
Now if we knew the height of the rectangles, we could figure out their area. Counting rectangles from the left edge of the region at x = 1, the 1st rectangle starts at x = 1, and so, since y = x, has height 1; the 2nd rectangle starts at x = 1 + Δx and so has height 1 + Δx. Similarly, the 3rd rectangle starts at x = 1 + 2Δx, and in general the i^th starts at 1 + (i-1)Δx.

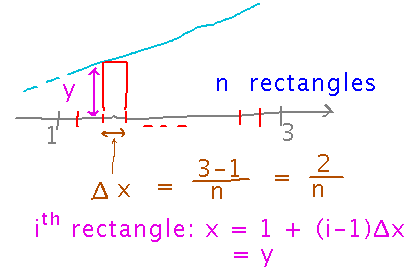
Now we can figure out the area of the i^th rectangle by multiplying its height by its width:

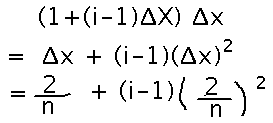
And finally, adding up the areas of all the rectangles gives an estimate of the total area under the line:

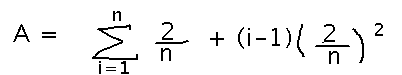
To do this calculation, we still have to calculate lots of little areas and add them all together. It would be nice not to have to do that, to just have a formula we could plug n into and get an answer (a “closed form”). But we’ve started to learn some rules for simplifying sums, so maybe we can simplify this one into a nice closed form.

A good place to start is to break the sum into 2 parts, using the rule that summing a sum (or difference) of terms is equal to summing each term separately and then adding the sums:

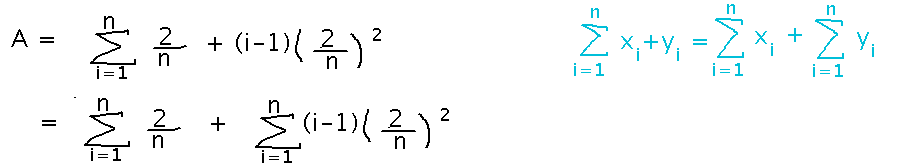
Next, realize that 2/n and (2/n)² are constants in these sums, they don’t change as the summation variable i changes. So they can be factored out of the sums:

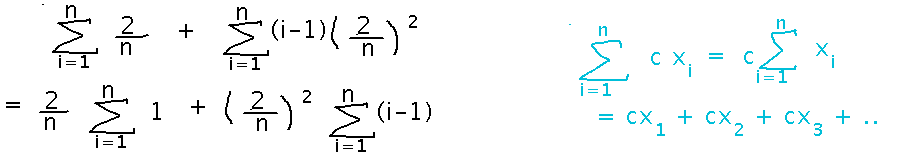
Next, split the sum of i-1...

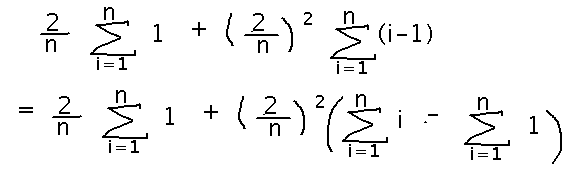
Now the only sums left in the formula are ones that have standard closed forms, e.g., closed forms available from tables in the textbook:

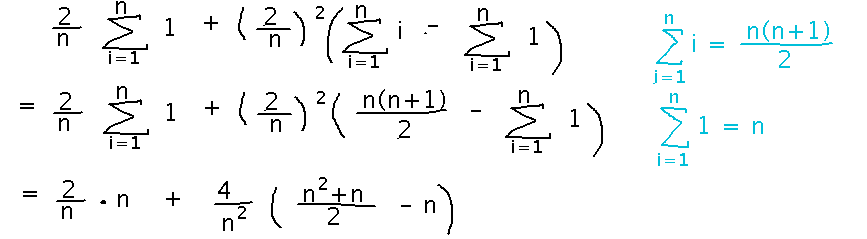
We’ve eliminated all the sums now. In principle we could plug any number of rectangles we liked, n, into this formula and calculate the total area inside all of them. But simplifying the formula can make that even easier:

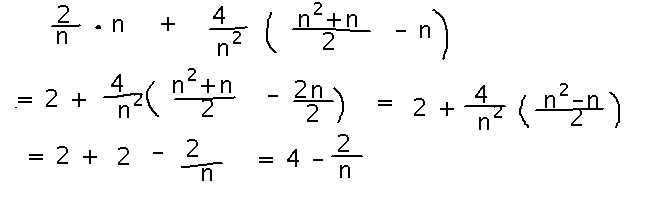
Now we have truly simple formula to calculate the total area inside any number of rectangles under y = x that we like. But plugging any finite number into this formula will still miss a little bit of area. What we’d like for ultimate accuracy is an infinite number of rectangles. We can’t do exactly that, of course, but the next best thing is the limit as n approaches infinity — which does, in fact, give the exact area:

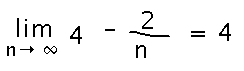
Process for Area Under a Graph

Approximate the area between the x axis and the graph of f(x), between x = a and x = b, as a sum of the areas of n rectangles.

1. Find the width of each rectangle: (b - a)/n
2. Find the height of each rectangle: f(x_i) where x_i is any x value in the i^th rectangle
3. Formula for total area is the sum of f(x_i) (b - a)/n
4. Simplify that sum
5. Take the limit as n goes to infinity. That will be the exact area.

The sum built in steps 3 and 4 is a called a “Riemann sum.”

The limit of the Riemann sum as n approaches infinity, in step 5, is the definite integral of f(x) between x = a and x = b.

Problem Set

See handout for details.

Next

A definite integral example, and properties of definite integrals.

Read the rest of section 5.2.

Next Lecture