Definite Integrals, Part 2

Misc

Colloquium on Thursday (April 25), 2:30 - 3:30, Welles 138

Prof. Sedar Ngoma

“An Introduction to Finite Difference Methods”

Extra credit for reflection/connection paragraphs.

Questions?

Definite Integrals and Riemann Sums

Section 5.2.

We saw one example Friday: the area between the graph of y = x and the x axis, from x = 1 to x = 3, is a definite integral.

Another Example

Find the integral from 0 to 2 of x³ as a limit of a Riemann sum.

The basic idea is that the integral represents (among other things) the area under the graph of x³ between x = 0 and x = 2. But as we saw last week, that area can also be approximated as a sum of many rectangles:

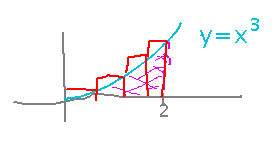
In fact, the area is calculated ever more exactly as the number of rectangles increases, and in the limit as the number of rectangles becomes infinite, the sum gives the exact area. So we have two equal ways of looking at the same thing:

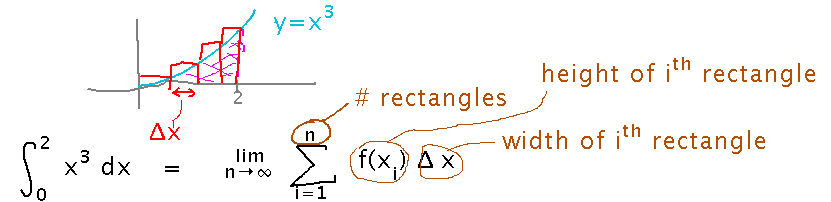
Realize that Δx, the width of each rectangle, is just the width of the whole interval from 0 to 2 divided by n, i.e., 2/n. Then pick x_i, the x value in the i^th rectangle, to be the right edge of that rectangle, so that x_i is just i times Δx. This lets us fill in lots of parts of the sum for this particular problem:

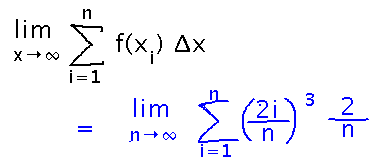
A good next step is to do the multiplications inside the sum:

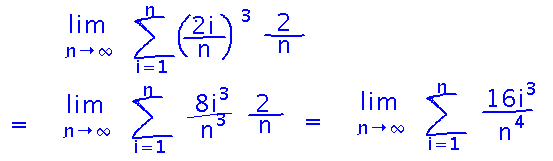
Then factor all the constants out of the sum:

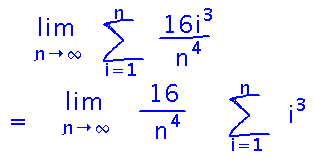
This leaves us with a sum of i³. There’s a good chance that such a simple sum has a known closed form (at least known to textbook authors and Google), so see if we can look it up. In fact, there’s a rule for it in our book. Use that rule to eliminate the sum altogether:

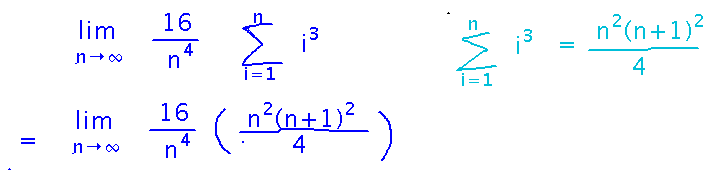
Now simplify...

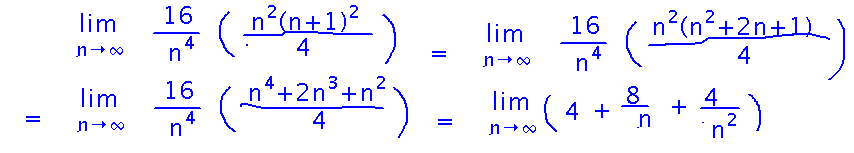
And finally we can take the limit, since in the simplified form all the terms with n go to 0 as n goes to infinity:

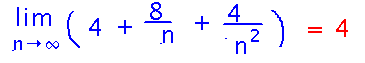
Here’s the complete record of how all this looked by the time we finished it in class:

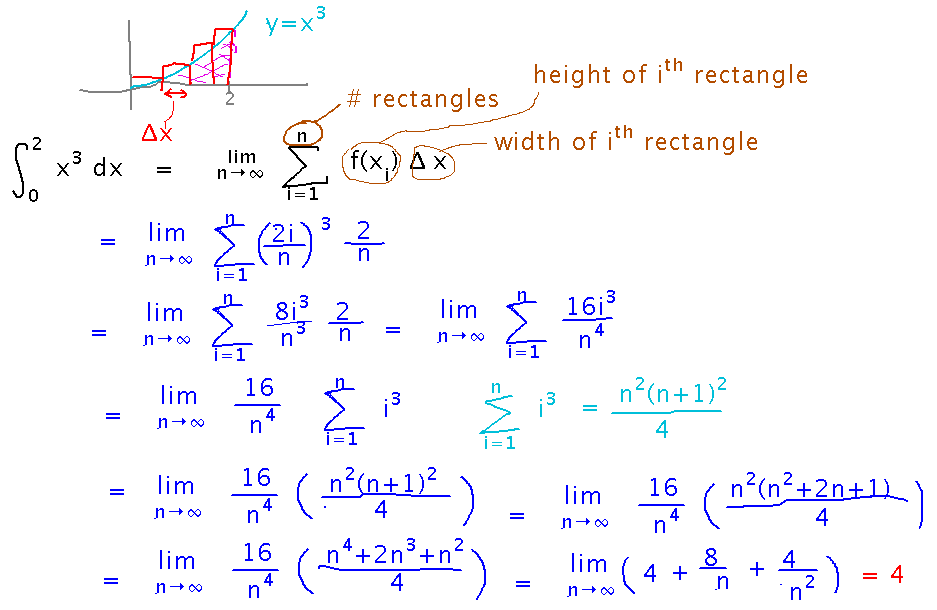
Summary

(A more general version of the process we identified last Friday for evaluating the area under a graph.)

To evaluate the definite integral of f(x) from x = a to x = b as a Riemann sum...

1. Set the problem up as the limit as n goes to infinity of the sum from 1 to n of f(x_i) Δx. Δx will generally be the width of the interval from a to b divided by n, i.e., (b-a)/n, and x_i can generally be a + i Δx.
2. Simplify the expression inside the sum; if that expression contains additions or subtractions, splitting it into multiple sums may be helpful.
3. Factor constants out of the sum(s); there will generally be constants involving n or its powers.
4. Find a closed form for the remaining sum; quite likely this will be a standard one that can be looked up.
5. At this point all that should left is a limit of some expression with no sum in it. Simplify that expression; terms involving n that were factored out of the sum in step 3 will likely (partially) cancel with terms involving n from the closed form of the sum.
6. Take the limit; it’s likely that terms involving n in this limit will all go to 0.

Next

Some properties of integrals you can use to (sometimes) avoid having to evaluate Riemann sums.

Read the “Properties of the Definite Integral” subsection of section 5.2 if you haven’t already.

(Then eventually, how to evaluate definite integrals without Riemann sums at all.)