Review

Return to Course Outline

Previous Lecture

Misc

The related rates problem from the test.

The question describes a garage or similar building with a raisable door, and a streetlight that shines through the opening as the door rises. You need to figure out how fast the length of the illuminated part of the floor is increasing.

A good way to start this problem is to figure out x (the length of the illuminated part of the floor) in terms of y (the height of the door opening). Do this from a realization that there are similar triangles in the problem:

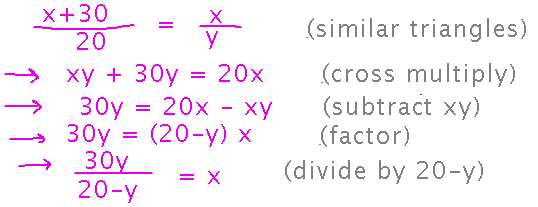
Once you know x in terms of y, differentiate with respect to t (time) to find how fast the illuminated region is increasing:

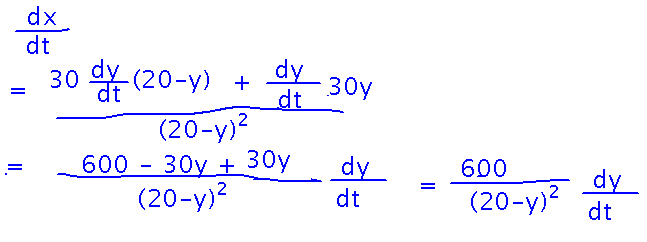
A finally you can plug in the known values for y and dy/dt to get a number. (But be careful not to plug in y and dy/dt before you take the derivative, because doing that will incorrectly make it look like x is a constant and so its derivative is just 0.)

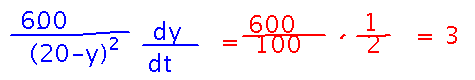
Here’s the work on this problem in a single image, more or less as it looked when we finished doing it:

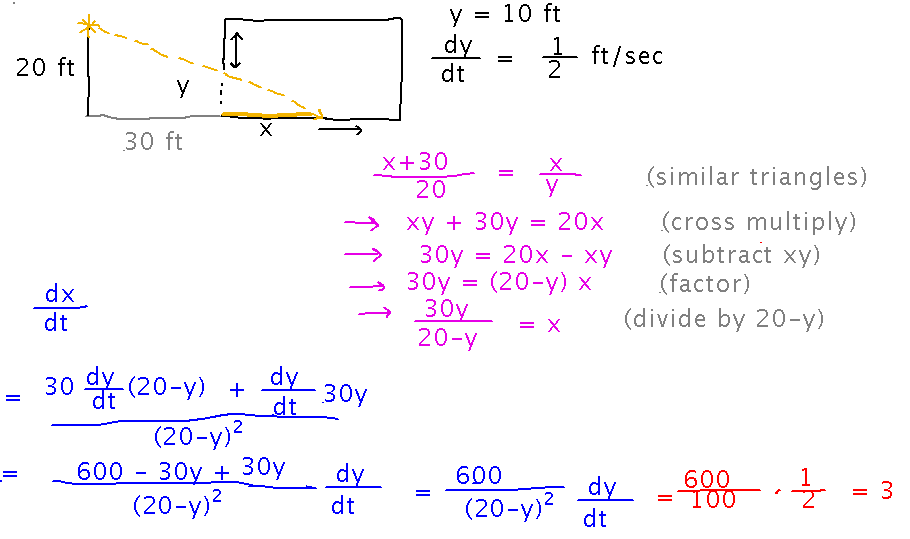
Questions?

Continuity

Continuity over an (open) interval: means the function is continuous at all points in the interval.

Recall that f(x) is continuous at a if...

• f(a) defined
• lim_x→a f(x) is defined
• f(a) = lim_x→a f(x)

For continuity over an interval, inspect f(x) for features that would make it undefined somewhere in that interval (e.g., denominators that could become 0). If none, f(a) is defined for all a in the interval.

Then check for places where limits can be different when approaching from the left and right. If there are none, and if f(x) is defined everywhere, then the limit can always be found using limit laws, and they will tell you the limit as x approaches a is f(a). So you get the second two requirements for continuity together.

Mathematica

How to use Mathematica to solve the shortest-wires problem (question 5 on the current problem set)?

See the picture in the book for the problem description and variable definitions.

Work out the length of the wire in terms of x by hand. Then put that formula into Mathematica as a function, take its derivative, and solve for values of x that make the derivative 0. Remember to check the endpoints of the interval x can lie in to make sure one of them isn’t the absolute minimum.

Here is a Mathematica notebook we developed to explore these ideas. (Be sure you understand it thoroughly when you come to grade.)

Speeder

How to answer Part B of the problem set question about the speeding driver (question 1)?

It starts with Part A, where the police don’t see the driver speeding, but can infer it via the Mean Value Theorem because the average speed (average derivative of distance) is greater than the speed limit.

But the Mean Value Theorem relies on the function in question being continuous, which distance isn’t for a teleporting car. So if the car has “teleport drive,” the police can’t use the Mean Value Theorem to infer speeding any more.

Next

Areas and definite integrals.

Next Lecture