SUNY Geneseo Department of Mathematics
Wednesday, April 10
Math 221 03
Spring 2019
Prof. Doug Baldwin
PRISM’s calculus bee is today (Wednesday), 2:30 - 3:45, Newton 201.
Tomorrow (Thursday).
Covers material since first exam (e.g., implicit differentiation, related rates, initial value problems, linear approximation, extreme values, shapes of graphs — roughly the material on problem sets 5 and 6).
Rules and format otherwise similar to first exam, especially open-references, open-calculator/computer, rules.
Practice exam now on Canvas.
Extended SI session today, 3:00 - 6:00, Bailey 209
Section 4.7
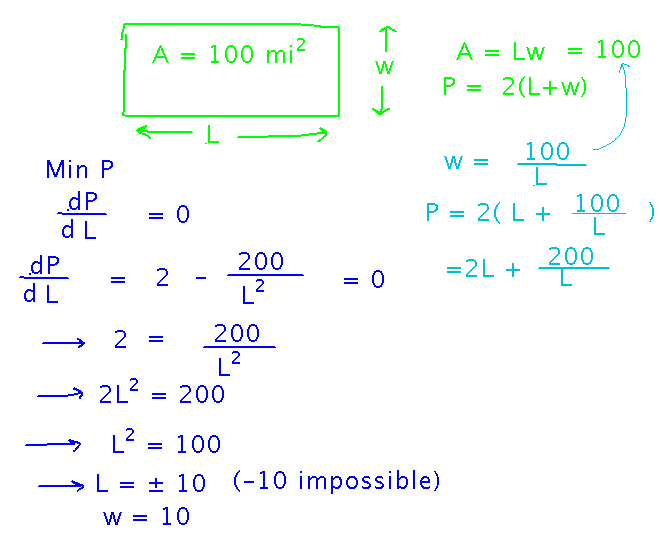
What is the minimum perimeter that a 100 square mile rectangular nature preserve can have?
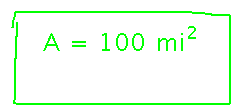
Start by naming the key quantities in the problem and finding equations that relate them. Here, for example, that would be the length, width, area, and perimeter of the preserve, and the formulas for area and perimeter in terms of length and width.
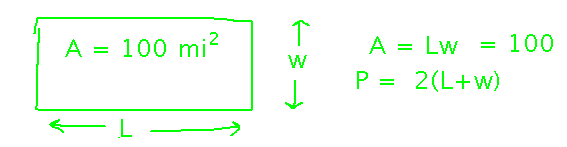
Now we want to find where perimeter is minimized, so we could set the derivative of perimeter to 0 and solve, except perimeter depends on 2 variables — so how to take a derivative of such a thing? Use the area to express one of length or width in terms of the other, then use that in the perimeter equation so it becomes an equation with just one variable:
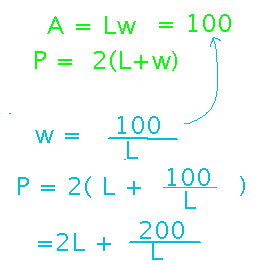
Now we can find the length for the preserve that minimizes its area. And once we have the length, we can calculate the corresponding width from it:
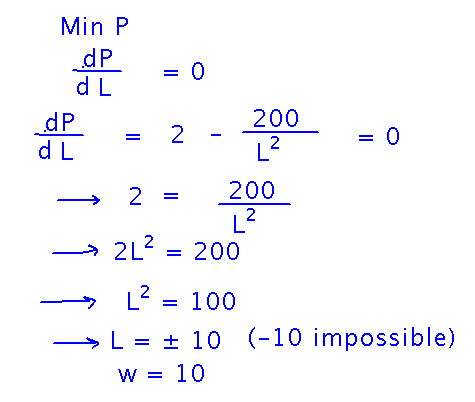
Here’s the complete process as it looked when we finished:
We can also graph perimeter as a function of length to get a visual sense that we did indeed find a minimum, and found it at a plausible place. Here’s a Mathematica notebook that does that.
Define the problem (picture, labeling variables, finding equations)
Use equations to express optimized quantity (Y) in terms of just 1 variable (x)
Differentiate Y with respect to x
Solve dY/dx = 0 for the optimal x
Calculate other variables from x
I have a piece of lawn 100 feet by 300 feet. When I mow it, the lawn mower of course ends up at the corner diagonally opposite the shed where it lives. I can push it across the grass at a speed of 4 feet/second, but along the driveway at a speed of 12 feet/second. What’s the fastest route to the shed to put the lawn mower away?
As before, start by defining variables to represent key quantities and equations that relate them. Two key quantities here are the distance I have to push the mower across the grass, and the distance I push it along the driveway. Distance along the grass comes from the Pythagoren Theorem. What I want to minimize is the time I spend pushing, which can be calculated from the two distances and the corresponding speeds.
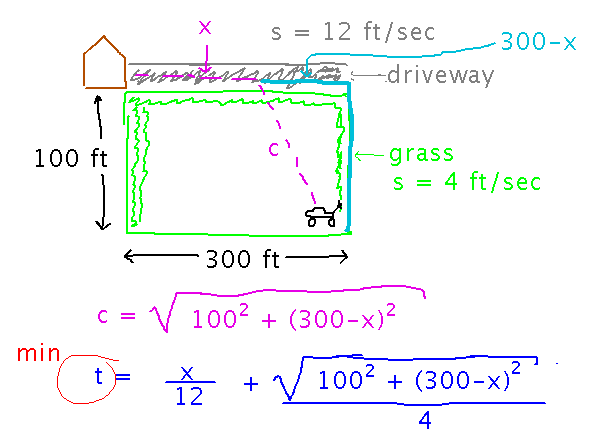
This is the set-up we finished class with. Find the actual place I should hit the driveway Friday, and also look at using Mathematica on a problem such as this.
(Friday, after exam)
Finish optimization
Bring computers to try out Mathematica solution.