SUNY Geneseo Department of Mathematics

The End Behavior of Functions, Part 2

Monday, April 8

Math 221 03
Spring 2019
Prof. Doug Baldwin

Misc

Exam 2 coming up Thursday (April 11).

Covers material since first exam (e.g., implicit differentiation, related rates, initial value problems, linear approximation, extreme values, shapes of graphs — roughly the material on problem sets 5 and 6).

Rules and format otherwise similar to first exam, especially open-references, open-calculator/computer, rules.

Practice exam now on Canvas.

Extended SI session Wednesday April 10, 3:00 - 6:00, Bailey 209

Questions?

End Behavior

Section 4.6.

Example with Graphing

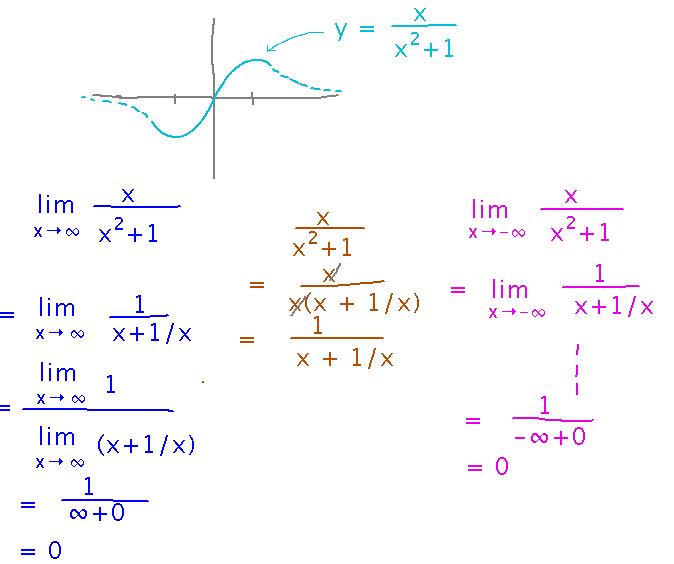
What does y = x / (x² + 1) look like at its left and right ends?

We decided that the key thing was to find limits as x approaches positive or negative infinity.

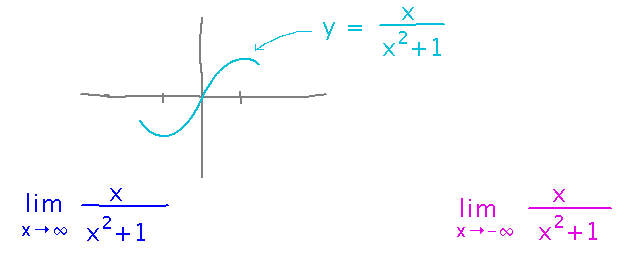
Plot of sinusoidal curve near origin and it's limit expressions as x goes to plus and minus infinity

Strange as it may seem, factoring x out of the numerator and denominator here is a good way to proceed. It allows us to cancel out the x in the numerator, getting rid of the ∞/∞ problem in the limit, and leaving terms in the denominator that are easy to take limits of at infinity.

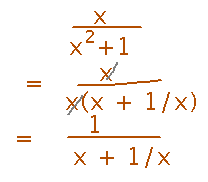
Factor x out of denominator x squared plus 1 to get x plus 1 over x

Now substitute this rewritten expression into the limit as x approaches positive infinity, and either use limit laws to simplify to terms whose limits we know, using the somewhat intuitive idea that 1/∞ becomes 0, or, more formally, noting that 1/(x + 1/x) can be made arbitrarily close to 0 by making x big enough, which is the formal definition of a limit at infinity.

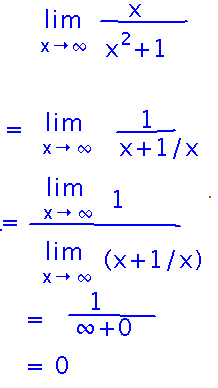
Limit of x over x squared plus 1 becomes limit of 1 over x plus 1 over x which is 0

Similar thinking applies to the limit as x approaches -∞:

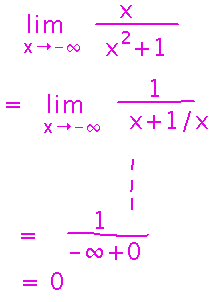
Limit as approaches minus infinity also becomes 0

So we conclude that the left and right ends of the graph level off at y = 0. Here’s the complete picture as it was when we finished with it in class:

Sinusoidal curve extended to decay towards 0 at ends, with limit calculations

Another Example

What is the limit as x approaches ∞ of y = (x²+1) / x?

Approach this similarly to the first example, namely by factoring x out of the numerator and canceling the denominator. The result is simpler than the first example to find limits of:

Limit of x squared minus 1 over x simplifies to limit of x minus 1 over x which is infinity

Key Points

Avoid ∞/∞

You can often avoid it by factoring the highest common power of x out of numerator and denominator. Then use the following rules, applying limit laws as needed to isolate the necessary forms:

Rules for limits at infinity
Function	Limit as x Approaches ∞	Limit as x Approaches -∞
xⁿ, n is positive & even	∞	∞
xⁿ, n is positive & odd	∞	-∞
1/xⁿ, n is positive	0	0
Constant	Constant	Constant

Optimization: extreme values with constraints.

For example, it’s good to minimize the perimeter of nature preserves, because that perimeter is what pests, poachers, etc. enter through. So what’s the minimum perimeter a rectangular nature preserve of 100 square miles can have?

Read section 4.7.

Next Lecture