Optimization, Part 2

Return to Course Outline

Previous Lecture

Misc

GREAT Day

Day-long celebration of student research, art, etc.

Next Wednesday (April 17).

No class that day.

Lots of math talks and posters; go see them (and other things, too).

Extra credit for writing reactions/reflection on any one math-related presentation.

No SI Today

Regular schedule resumes next Friday.

(No SI Wednesday for GREAT Day.)

Questions?

Optimization

Section 4.7.

Lawn Mowing by Hand

Last time we saw my lawn mowing problem, in which I want to figure out where to arrive on the driveway in order to have the fastest trip from the corner of the lawn to the shed:

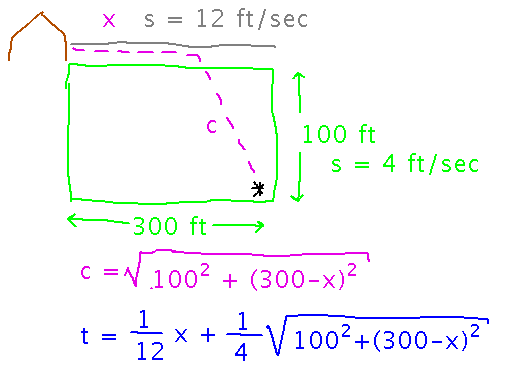
We had decided to call the distance I push the lawnmower across the driveway x, and the distance I push it across the grass c. We realized that the Pythagorean Theorem gives us c in terms of x. Finally, we worked out the total time to get to the shed by dividing the distances by the speeds at which I move on the respective surfaces.

What’s left is now to take the derivative of t and solve for the x value that makes it 0. The biggest trick in taking the derivative is to realize that square root can be thought of as raising something to the 1/2 power, so the big square root in this problem can be handled via the power rule and several uses of the chain rule. Once we do that, the result simplifies fairly nicely.

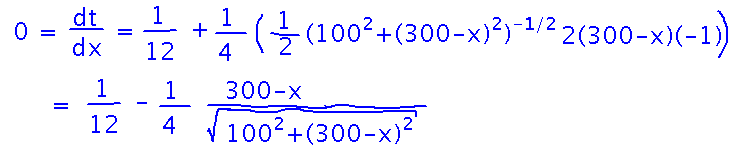
Now actually solving for the x that makes this 0 involves lots of algebra, but isn’t too bad. Especially since we left (300-x)² as (300-x)² instead of FOILing it out, which turns out to make the algebra easier later in this process:

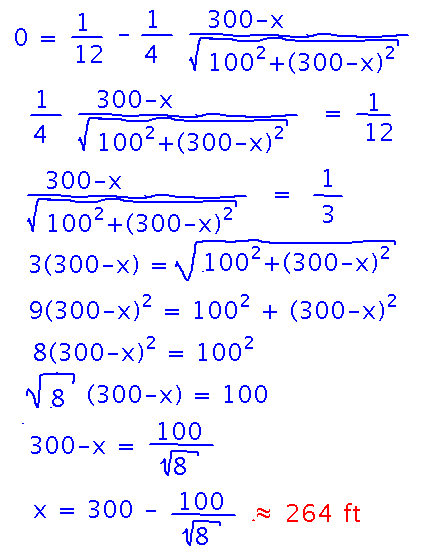
Here is the whole problem solution in a single picture, more as it appeared in class at the end (and as it would have appeared if there had been space for it all on a single screen on the projector):

To do a complete job on this problem we should also check that the endpoints of the interval x must lie in, namely from 0 to 300, don’t produce smaller values, although they won’t because for x < 264, say 0, the derivative is negative, and for larger x, say 300, the derivative is positive, so we know we have a local minimum. But for completeness’s sake, if I go straight from the corner of the lawn diagonally across the grass to the shed (x = 0 feet) my time is about 79 seconds, whereas if I go up the edge of the lawn to the driveway and then to the shed (x = 300 feet) my time is 50 seconds, and on the path calculated above (x = 264 feet) my time is about 49 seconds.

Lawn Mowing with Mathematica

This problem is also a good example of the kind of situation in which you can solve an entire problem in Mathematica (or another technology tool). This notebook contains the work we did while demonstrating that approach.

Key ideas included

• Giving certain key things in the problem (namely the time function and its derivative) names in Mathematica for easy use later. See the := commands.
• Using Mathematica’s built-in Solve function to find x values where the derivative is 0.
• Carrying out the whole process as a series of Mathematica commands (as opposed to earlier Mathematica examples, where we have generally been able to do what we wanted in just one command).

Next

Area under curves.

Read section 5.1.

Next Lecture