Misc
Exam 2
Coming up next Thursday (April 11).
Covers material since first exam (e.g., implicit differentiation, related rates, initial value problems, linear approximation, extreme values, shapes of graphs — roughly the material on problem sets 5 and 6).
Rules and format otherwise similar to first exam, especially open-references, open-calculator/computer, rules.
Practice exam forthcoming.
Extended SI session Wednesday April 10, 3:00 - 6:00, Bailey 209
SI Session
3:00 this afternoon, Bailey 209.
Questions?
Wrapping Up Shapes of Graphs Contest
Yesterday we saw...
- Orion’s Belt
- Kite
- Airplane
- “Heart of Sadness”
- Heart
Any others?
Vote for the one(s) you thought most creative yet precise in matching derivatives to shape.(The winner was the airplane.)
Key Points
f′(x) < 0: graph is decreasing
f′(x) > 0: graph increasing
f′′(x) < 0: graph is concave down
f′′(x) > 0: graph is concave up
For example, when the derivative is getting bigger, indicated by pink tangent lines here, the graph bends upward, i.e., speeds up its increase, or at least slows down its decrease. Similarly, if the derivative is getting smaller (brown tangent lines), the graph bends downward.
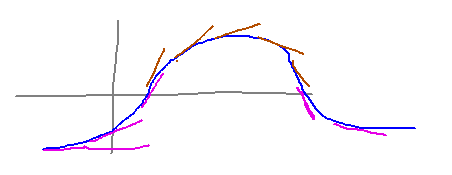
...and here is the above graph with the function’s derivative and second derivative included:

(Here is the picture from the above discussion as actually displayed in class:)
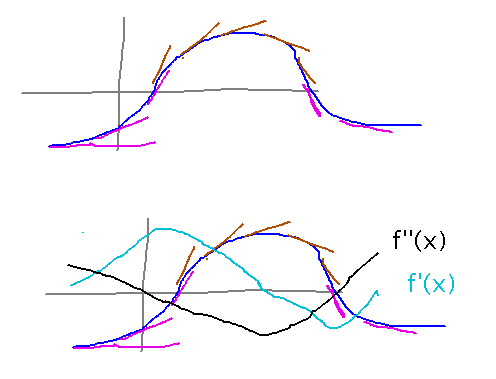
End Behavior
Section 4.6
Examples
What does y = x / (x2+1) look like as x gets very large? How about as x gets very negative?
Around the origin, the function has a minimum at x = -1 and a maximum at x = 1.
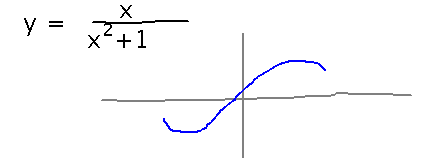
But what should I draw far away from these points? Figuring out the limit of y as x approaches infinity and negative infinity can help here. But it’s not immediately clear what that is either — if we try to plug infinity (or negative infinity) in for x in the definition of y we get infinity over infinity, an undefined value (this is a consequence of infinity not really being a number we can do arithmetic with).
Like previous limits that were undefined when plugging a value in for x, see if we can use algebra or limit laws to rewrite this one in a form that is defined. In doing this, some special rules for limits as x approaches infinity (or negative infinity) can help (these rules can be proven from the formal definition of limit as x approaches infinity or negative infinity):
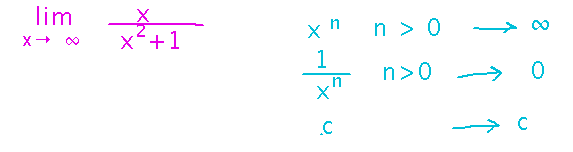
(The complete picture for this discussion, as seen in class, is...)
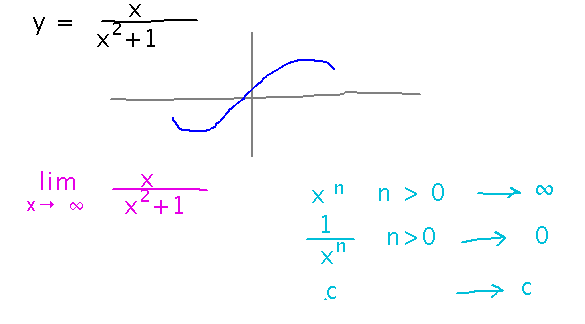
Next
Finish using limit laws and algebra on the above example, and probably some more.