Extreme Values, Part 2

Return to Course Outline

Previous Lecture

Misc

Colloquium

Next Tuesday, April 2, 2:30 - 3:30, Welles 138.

Chris Leary (Geneseo), on “Learnability Can Be Undecidable”

Extra credit for going and writing around 1 paragraph on connections you make or reactions you have.

SI Sessions

Back to normal schedule now, i.e., this afternoon (and other Wednesdays) 3:00 - 4:30, Friday 3:00 - 4:30.

Mid-Semester Feedback Questionnaire

Return by Friday (if you choose to do it).

Questions?

Shadow Problem

Hints or ideas on the problem set question about the length of a person’s shadow as they walk away from a lamp (question 4)?

Here’s the basic scenario: a person 6 feet tall is walking away from a 10 foot tall lamppost, and casting a shadow. The question has 2 parts, one asking how fast the tip of the shadow moves away from the person, and the other asking how fast the tip of the shadow moves away from the lamppost. To talk about these problems, call the distance from the person to the tip of the shadow x, and the distance from the lamppost to the person y.

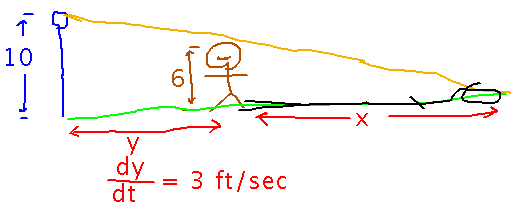
In terms of these variables, the first part of the question is asking for dx/dt. The second part is asking for the rate of change of the sum y + x, which sounds weird at first, but isn’t so bad when you realize that a derivative of a sum is just the sum of the derivatives (the sum rule).

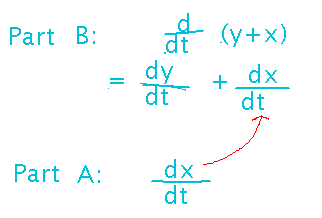
You can use similar triangles to solve the first part of the problem, starting with ratios between the lengths of the sides of the person-and-ground and lamppost-and-ground triangles, then rearranging to isolate x, and finally differentiating. Note at the end that the problem gives you the rate of change for y, the distance from the lamppost to the person.

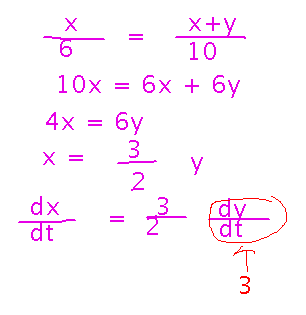
Speeding Car Problem

Hints on the problem set question about a speeding car (question 1)?

See the discussion from Friday’s class before break. That gives a diagram of the problem, and realizes that it’s an initial value problem, using the idea that distance is the integral of speed.

Plotting Implicit Curves

How to plot the curve x²y = y - 7 from question 2?

Use Mathematica’s ContourPlot function, as demonstrated in this notebook.

Extreme Values

Section 4.3.

Summary so Far

To find extreme values of function f(x) over interval [a,b]...

1. Find f′(x).
2. Solve for the x values that make f′(x) = 0
3. Identify any x values for which f′(x) is undefined
4. X values from (2) and (3) can correspond to extreme values; evaluate f at each to get a y value
5. Evaluate f(a) and f(b) to get y values
6. The largest and smallest y values from (4) and (5) are the absolute maximum and minimum of f on interval [a,b]; other y values may correspond to local maximums or minimums.

A Pitfall

Find the critical points of y = x³.

You might think you could just find an x that makes dy/dx 0 and be done. But beware! The theory behind why you find critical points in order to locate maxima and minima says that if there is a maximum/minimum, then it happens at a critical point. It does not say that every critical point is a maximum or minimum (just as I can offer someone $10 if they give me a water bottle without implying that giving me the water bottle is the only reason I might give them $10).

y = x³ doesn’t have a minimum or maximum, despite having a 0 derivative at x = 0. Points where this happens are called “inflection points.”

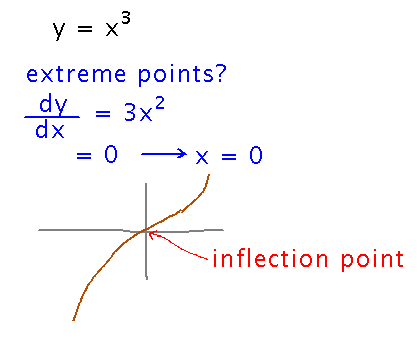
Next

More examples of extreme value problems.

Next Lecture