Extreme Values, Part 3

Return to Course Outline

Previous Lecture

Questions?

Extreme Value Examples

Radio Example

A simplified model of how your television (or radio, cell phone, wifi connection, etc.) knows what radio frequency to listen to (as opposed to all the other frequencies it ignores).

An electrical circuit whose “impedance,” z, (opposition to electricity flow) varies with frequency, f, according to

z = f / (1+f²)

(In real life there are coefficients attached to the f’s, and the 1 might be some other constant — that’s why this is a simplified model.)

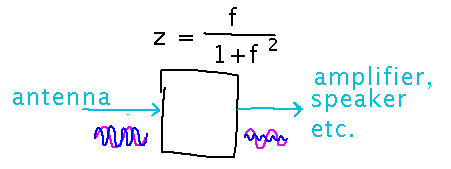
Where does this circuit have maximum impedance?

Values of f where dz/df is 0 will be possible maxima/minima. So start by finding that derivative:

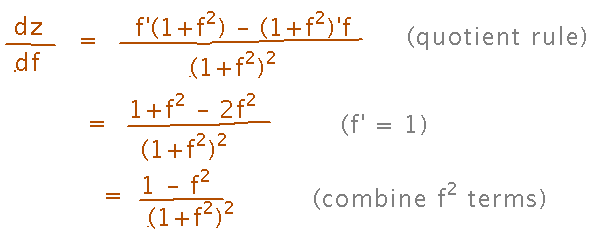
Then solve for the f value(s) that makes the derivative 0:

So minimum or maximum impedance will happen when f = 1 (-1 is physically impossible for a frequency). But is that a minimum or maximum? Since we know f = 1 is the only critical point and we’re looking over all possible values of f, we can just plug a few numbers near 1 into the formula for z and see if they produce values larger or smaller than z at 1:

• z(0) = 0
• z(1) = 1/2
• z(2) = 2/5

So z(1) is where impedance is maximized.

Golf Ball Example

Imagine a golf ball hit into the air in such a way that it’s height (relative to where it was when hit) t seconds after being hit is h(t) = 50t - 16t² feet. The ball lands after 2.9 seconds on the side of a hill (i.e., higher than where it started).

What are the highest and lowest heights the ball reaches during this flight?

One big distinction between this problem and the radio one is that here we’re looking for extremes in an interval, specifically 0 ≤ t ≤ 2.9.

But we can still start by identifying critical points based on the derivative of h:

Now, since there are finite endpoints to the interval, we need to see if the minimum or maximum height occurs at one of them (intuitively the minimum occurs at t = 0 because height there is 0, and the ball can’t have a negative height — unless it falls into a hole or something).

Spring Example

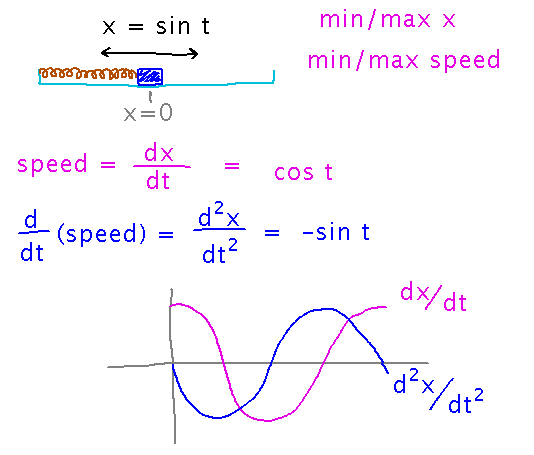
A weight pushed back and forth by a spring has position x relative to its initial position, given by x = sin t where t is time.

When does the weight reach its maximum and minimum positions?

When does it reach its maximum and minimum speeds?

There are a couple of interesting things here, including that speed is the derivative of x, so since maximum and minimum x occur when it’s 0, the largest x displacements occur when the speed is smallest. Also, speed and its derivative (and position and its derivative) are all similar sine-like curves, just displaced relative to each other. So speed and position have similar oscillations, but maximum and minimums occur at different times.

Key Points

When finding extreme values over all reals (e.g., radio example), look for critical points.

When finding extreme values over an interval (e.g., golf example), look at critical points and endpoints.

Next

Put some intuition about what derivatives mean on a firm footing in order to better distinguish maximums from minimums, and gain more insight about the shapes of graphs.

The Mean Value Theorem.

Read section 4.4

Next Lecture