SUNY Geneseo Department of Mathematics
Thursday, March 14
Math 221 03
Spring 2019
Prof. Doug Baldwin
The problem we started yesterday, with a pedestrian and a car approaching a crosswalk. We wanted to know what dz/dt is, i.e., how fast the straight-line distance between the pedestrian and the car is changing. That distance is given by the Pythagorean Theorem.
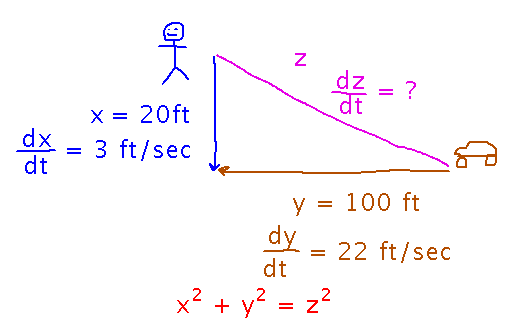
We came up with two ways to find dz/dt. the first solves for z in terms of x and y and then differentiates, which is straightforward but requires using the power rule with a fractional exponent, which technically we have never proven works. Nonetheless, completing that solution by plugging in numbers for x, y, and their derivatives gives an answer:
The other approach is to implicitly differentiate the equation for z2 in terms of x2 and y2, which is subtler but doesn’t rely on any unproven math. That method produces the same answer:
Super spy Jane Bond is hiding under the wall to Dr. Doom’s estate, trying to avoid the estate’s security camera. The camera is on a telescoping pole. How fast does the region below the wall where Jane Bond is safe from the camera change as the camera’s height changes?
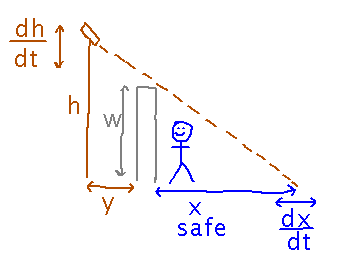
The key idea for connecting the safe region to the camera’s height is to realize that there are 2 similar triangles in this problem: one defined by the safe region and the wall, and the other defined by the safe region plus the pole’s distance inside the wall and the camera’s height:
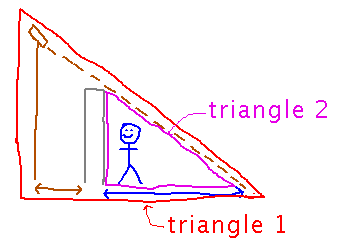
Because the triangles are similar, ratios of corresponding sides are equal:
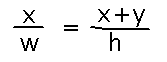
Now we can rewrite this equation to give x in terms of h (and w and y, which are constants):
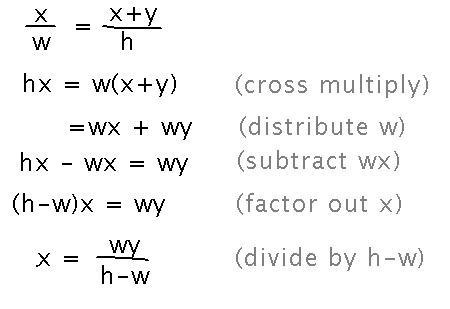
And finally we can take derivatives:
See handout for details.
Approximation with derivatives.
Read section 4.2