SUNY Geneseo Department of Mathematics

Related Rates, Part 1

Wednesday, March 13

Math 221 03
Spring 2019
Prof. Doug Baldwin

Return to Course Outline

Previous Lecture

Misc

SI this afternoon: 3:00 - 4:30, Bailey 209.

No SI Friday.

Questions?

Related Rates Problems

Section 4.1.

Drone Example

Imagine a drone with a camera, the camera takes square pictures with a ±10 degree field of view.

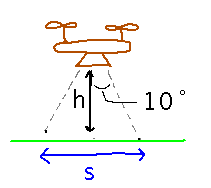
Drone flying at height h above region of width s

How fast does the area photographed change with the drone’s changing height?

If height = 100 ft and the drone is rising at a rate of 2 ft/sec, what is the actual numeric rate of change in area photographed?

Noticing that half of the square’s width and the drone’s height define the lengths of 2 sides of a right triangle, with the 10 degree angle opposite the half width, gives us a way to relate height and size of photo:

Starting with tangent of 10 degrees, solve for area

Now, differentiating both sides of the area equation gives the derivative of area in terms of height and its derivative:

Derivative of area is a function of height and height's derivative

Finally, we can plug in the actual numbers for height and its rate of change to get a specific numeric answer:

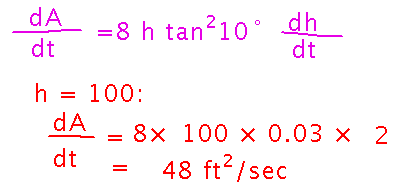
Plugging in specific height and derivative gives specific derivative of area

Summary of what we did

  1. Find an equation for the quantity whose derivative we’re interested in (area) in terms of other values in the problem.
  2. Differentiate.
  3. Plug in numbers.

Traffic Example

(A “real-world math bounty” suggestion from a past semester.)

A pedestrian and a car are both approaching a crosswalk a right angles to each other. If the pedestrian is 20 ft from the crosswalk, walking at a speed of 3 ft/sec, and the car is 100 ft from the crosswalk traveling at 22 ft/sec, how fast is the distance between the pedestrian and car changing?

Once again, start by setting up equations. This time there’s no diagram, so drawing one and labeling it with the various variables is a good start:

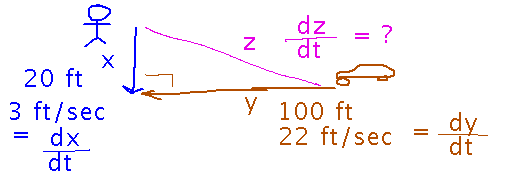
Pedestrian and car paths are two sides of a right triangle

Now find an equation for z, the distance whose derivative we want. The Pythagorean theorem is a good source for this equation:

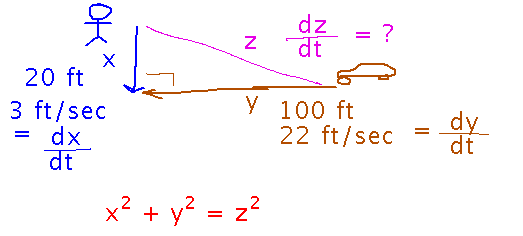
Pythagorean theorem gives distance from pedestrian to car in terms of each's distance from crosswalk

Now we need a derivative, which we could do in either of 2 ways. One is to take square roots on both sides of the equation for z2 to get an equation for z, and differentiate it. Note that taking that derivative assumes the power rule works for fractional powers, and we haven’t actually seen that it does yet. The resulting derivative is also kind of messy:

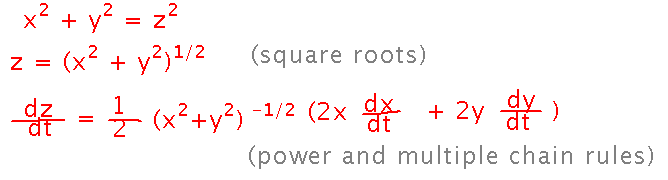
Derivative of square root of x squared plus y squared uses chain rule several times

The other way would be to implicitly differentiate the z2 = x2 + y2 equation, and isolate dz/dt.

Next

Finish the traffic example, and try some more related rates problems.

Complete one or the other (or both) of the ways of solving the traffic example for tomorrow, and be ready to describe or ask questions about what you did.

Next Lecture